Question 1152153: There is a mountain with 30 bat caves in a row that contain 340 bats in all. Any 7 caves in a row contain exactly 77 bats. Suppose the first cave has 7 times more bats than the last cave. How many bats are in the 29th cave?
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by ikleyn(52802)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
It is a nice problem, but formulated INACCURATELY.
An accurate formulation is THIS :
There is a mountain with 30 bat caves in a row that contain 340 bats in all.
Any 7 caves in a row contain exactly 77 bats.
Suppose the first cave has 7 times  as many bats as many bats  as the last cave.
How many bats are in the 29th cave? as the last cave.
How many bats are in the 29th cave?
Why it must be so, and why it can not be in different way, you will see, when you complete reading my solution.
Solution
Let me start my solution from the reference to an Internet dictionary
"in a row" means "in succession".
In this problem, it is the only meaning of this term.
1. Since any 7 caves in a row contain exactly 77 bats, we have, in particular
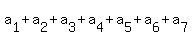 = 77, (1) = 77, (1)
 = 77. (2)
Subtract equation (1) from equation (2). The terms from = 77. (2)
Subtract equation (1) from equation (2). The terms from  to to  will cancel each other, and you will get will cancel each other, and you will get
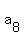 - -  = 0, or = 0, or
 = = 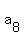 .
Making the same step by step, you will get .
Making the same step by step, you will get
 = =  , ,
 = =  , ,
 = = 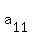 , ,
 = =  , ,
 = =  , ,
 = = 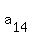 , ,
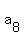 = = 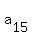 = =  and so on. It means that the sequence
and so on. It means that the sequence  , ,  , ,  , . . . , , . . . ,  is PERIODICAL with the period 7.
It is the FIRST IDEA of the solution.
2. Its consequence is that is PERIODICAL with the period 7.
It is the FIRST IDEA of the solution.
2. Its consequence is that  = = 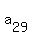 .
Therefore, from the condition, we have this equation .
Therefore, from the condition, we have this equation
 = = 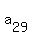 = =  . (3)
It is the SECOND IDEA of the solution.
3. From the condition, we have . (3)
It is the SECOND IDEA of the solution.
3. From the condition, we have
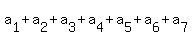 = 77, = 77,
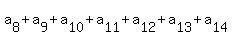 = 77, = 77,
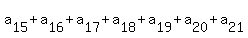 = 77, = 77,
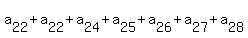 = 77.
since any 7 caves in a row contain exactly 77 bats.
Add these 4 equation (both sides). You will get = 77.
since any 7 caves in a row contain exactly 77 bats.
Add these 4 equation (both sides). You will get
 + +  + +  + . . . + + . . . + 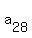 = 4*77 = 308.
It means that = 4*77 = 308.
It means that
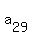 + +  = 340 - 308 = 32. (4)
It is the THIRD IDEA of the solution.
4. Now, from equations (3) and (4) we have = 340 - 308 = 32. (4)
It is the THIRD IDEA of the solution.
4. Now, from equations (3) and (4) we have
 + +  = 32.
It implies = 32.
It implies  = 32, or = 32, or
 = 32/8 = 4.
Hence, = 32/8 = 4.
Hence, 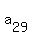 = =  = 7*4 = 28.
ANSWER. = 7*4 = 28.
ANSWER. 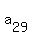 = 28. The 29-th cave has 28 bats. = 28. The 29-th cave has 28 bats.
Solved.
---------------
The solution by @MathLover1 is INCORRECT.
It is incorrect starting from its second line, where @Mathlover1 states that it follows from the condition
that each cave has 11 bats.
This statement is WRONG, and it DOES NOT FOLLOW from the condition.
|
|
|