SOLUTION: A young wizard knows every third spell that an old wizard knows. However, the young wizard knows two spells that the old wizard does not know. 8/9 of all the spells that the youn

Let  x = number of spells Old wizard knows;

     y = number of spells Young wizard knows;

     z = number of spells BOTH wizards know (intersection).


Then from the condition, you have these equations


     z = ,               (1)    (A young wizard knows every third spell that an old wizard knows.)

 
     y = 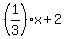;             (2)    (A young wizard knows every third spell that an old wizard knows. However, the
                                           young wizard knows two spells that the old wizard does not know. )


     z = 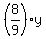.               (3)    (8/9 of all the spells that the young wizard knows are known to the old wizard as well.)


Thus we have three equations for 3 unknowns.


To solve the system, from (1) and (3) you have


      = ,

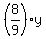which implies

     3x = 8y.                 (4)


From equation (2), substitute  y = 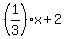  into equation (4).  You will get


    3x = 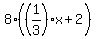.          (5)


Multiply both sides of equation (5) by 3


     9x = 8x + 8*2*3,    or

     x  = 48.


Then from  (1)  z = 16,  and from  (2)  y = 18.


Now the value under the question is  x + y - z = 48 + 18 - 16 = 50.    ANSWER

The problem says  "8/9 of all the spells that the young wizard knows are known to the old wizard as well".


It also says that  "the young wizard knows two spells that the old wizard does not know."


It means that  1/9  of the words young wizard knows is 2.


Hence, the number of words that young wizard knows is 18.


It means that the number of words that BOTH wizards know is  18-2 = 16.


In turn, it implies that the number of words the old wizard knows is  3*16 = 48.


And the answer to the problem question  is  then  48 + 18 - 16 = 50 - the same aa above.