Questions on Algebra: Average answered by real tutors!

Tutors Answer Your Questions about Average (FREE)

Question 1210373: Emilía has an average of 70 on 4 different tests. If the lowest score is dropped, her average rises to 90. What is the lowest score?
Found 3 solutions by math_tutor2020, greenestamps, josgarithmetic:
Answer by math_tutor2020(3816)   (Show Source):
You can put this solution on YOUR website!

x = sum of the three scores after the lowest score was dropped, i.e. we ignore the lowest score
x/3 = 90 = mean of those three scores
x = 3*90 = 270

y = lowest score that was dropped
x+y = sum of four test scores
(x+y)/4 = 70
(270+y)/4 = 70
270+y = 4*70
270+y = 280
y = 280-270
y = 10

Answer: 10

Answer by greenestamps(13198)   (Show Source):
You can put this solution on YOUR website!

4 tests with an average of 70; total points 70*4 = 280.

3 tests with an average of 90; total points 90*3 = 270.

The number of points on the test that is dropped is 280-270 = 10.

ANSWER: 10

Answer by josgarithmetic(39616)   (Show Source):
You can put this solution on YOUR website!

, assuming w is lowest score

But so many variables are not really necessary for this.

Let .

Question 1174226: A ladder 4m long at a construction site is resting against a wall. The bottom of the ladder is slipping away from the wall. Find the estimate of the instantaneous rate of change of the Height H of the top of the ladder with respect to the Distance D of the bottom of the ladder from the wall when the bottom of the ladder is 2.5m away from the wall. Use h = 0.01 as the central interval.
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website!
.
A ladder 4m long at a construction site is resting against a wall. The bottom of the ladder is slipping away
from the wall. Find the estimate of the instantaneous rate of change of the Height H of the top of the ladder
with respect to the Distance D of the bottom of the ladder from the wall
when the bottom of the ladder is 2.5m away from the wall. Use h = 0.01 as the central interval.
~~~~~~~~~~~~~~~~~~~~~~~~~

First, the problem in the post is posed INCORRECTLY.
To be correct, the problem must provide the rate of the horizontal move of the base of the ladder
from the wall, as the input data. Without this input data, the problem CAN NOT BE SOLVED.

Second, this instruction "Use h = 0.01 as the central interval" is IRRELEVANT to the problem.
By knowing the mathematical level of those who write to this forum, I am 837% sure
that this "instruction" came mistakenly from the other problem.

Third, the "solution" by @CPhill is non-sensical collection/soup of words.
It does not solve the problem, and even can not be a subject for discussions.
So, my advise to you is to ignore his post, for the sake of safety of your mind.

Now I am ready to start my solution.
I will assume, that the rate of the horizontal move of the base of the ladder
from the wall is 0.5 meters per second.

S O L U T I O N Let H be the height of the ladder (in meters) when it leans against the wall. Let D be the distance of the ladder base from the wall (in meters). Write the Pythagorean equation H^2 + D^2 = 4^2 = 16, (1) where '4' is the ladder's length, in meters. When the ladder moves, we consider H and D as functions of time; H = H(t), D = D(t). But the length of the ladder remains with no change. Differentiate equation (1) with respect to time, keeping in mind that the right side is a constant. You will get -D*D' 2H*H' + 2D*D' = 0, or H*H' + D*D' = 0, or H' = -------. (2) H Calculate H: H = 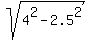= 3.1225 m (approximately). Recall that D' is given D' = 0.5 m/s. Substitute the values into formula (2) and get H' = = -0.40032 m/s. ANSWER. Thus the ladder's upper point moves down along the vertical wall with the rate of 0.4 m/s at the assigned time moment.

Solved correctly, with complete explanations.

For this class of problems, it is a standard methodology of their solution.

Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website!
Absolutely! Let's solve this problem step-by-step.
**1. Set up the Problem**
* **Ladder Length:** 4 meters (constant)
* **Distance from Wall (D):** 2.5 meters
* **Height on Wall (H):** We need to find this.
* **Rate of Change:** We want to find dH/dD (how the height changes with respect to the distance).
**2. Use the Pythagorean Theorem**
* We have a right triangle formed by the wall, the ground, and the ladder.
* The Pythagorean theorem states: D² + H² = 4² (where 4 is the ladder length)
* D² + H² = 16
**3. Express Height (H) in Terms of Distance (D)**
* H² = 16 - D²
* H = √(16 - D²)
**4. Find the Instantaneous Rate of Change (dH/dD)**
* We'll use the given central difference method to estimate the derivative.
* The formula for the central difference is:
* dH/dD ≈ [H(D + h) - H(D - h)] / (2h)
* Where:
* D = 2.5 meters
* h = 0.01 meters
**5. Calculate H(D + h) and H(D - h)**
* H(D + h) = H(2.5 + 0.01) = H(2.51) = √(16 - 2.51²) ≈ √(16 - 6.3001) ≈ √9.6999 ≈ 3.11446
* H(D - h) = H(2.5 - 0.01) = H(2.49) = √(16 - 2.49²) ≈ √(16 - 6.2001) ≈ √9.7999 ≈ 3.13048
**6. Substitute into the Central Difference Formula**
* dH/dD ≈ (3.11446 - 3.13048) / (2 * 0.01)
* dH/dD ≈ (-0.01602) / 0.02
* dH/dD ≈ -0.801
**Result**
* The estimated instantaneous rate of change of the height of the ladder with respect to the distance of the bottom of the ladder from the wall is approximately -0.801 meters per meter.
**Therefore, when the bottom of the ladder is 2.5 meters from the wall, the top of the ladder is sliding down the wall at a rate of approximately 0.801 meters for every meter the bottom slides away.**

Question 1151755: Two faulty tennis ball machines start to shoot balls from opposite sides of a 25
meter by 10 meter tennis court. The green ball machine shoots green balls that
stop on the court 5 meters to 20 meters from the green machine's side. The
yellow ball machine shoots yellow balls that stop on the court 2 meters to 16
meters from the yellow machine's side. Find the area of the tennis court that has
balls of either color on it.
Found 2 solutions by ikleyn, hudikamo:
Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website!
.
Two faulty tennis ball machines start to shoot balls from opposite sides of a 25
meter by 10 meter tennis court. The green ball machine shoots green balls that
stop on the court 5 meters to 20 meters from the green machine's side. The
yellow ball machine shoots yellow balls that stop on the court 2 meters to 16
meters from the yellow machine's side. Find the area of the tennis court that has
balls of either color on it.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

The balls cover the area from min(5, 2) = 2 meters to max(20,16) = 20 meters.

The length of this area is 20-2 = 18 meters.

Regarding the width of the area, the problem keeps silence about it,
but we can accept/admit that the width is equal to the width of the tennis court of 10 meters.

Thus the covered area is (or can be estimated as) 18 * 10 = 180 square meters.         ANSWER

Solved.

Answer by hudikamo(4)   (Show Source):
You can put this solution on YOUR website!
The Yellow Machine shoots balls over a distance of 14 metres (16-2), 9-23 m away from the green machine.
The Green Machine shoots balls over a distance of 15 metres (20-5), 5-20 m away from itself.
The overlapping area is defined from the Green Machine's nine metre line and 20 metre line, 11 metres wide.
The width of the court is 10 m. Total Area = 11*10 = 110 m^2

Question 1165911: The Sugar Sweet Company is going to transport its sugar to market. It will cost $4050 to rent trucks, and it will cost an additional $150 for each ton of sugar transported.
Let represent the total cost (in dollars), and let represent the amount of sugar (in tons) transported. Write an equation relating to , and then graph your equation using the axes below.
i also need to graph it and im not sure how....
Answer by hudikamo(4)   (Show Source):
You can put this solution on YOUR website!
A few symbols are missing but will try to solve:
Base cost = 4050. This is constant.
Additional cost = Amount of sugar (x) * 150
Let y represent total cost, and x represent amount of sugar.
Total cost = 150 tons of sugar + Base cost
y = 150x + 4050
The graph is difficult to properly visualize however it will pass through the y axis at (0,4050), and for every additional x value will raise its y value by 150
e.g for x = 1, 2, 3 y = 4300, 4450, 4600

Question 1210267: Matthias and Klara live in a high-rise building. Klara lives 12 floors above Matthias. One day, Matthias climbs the staircase to visit Klara. When the amount of floors he has traveled equals the number of remaining floors, he is on the 8th floor. On which floor does Klara live
Found 2 solutions by ikleyn, josgarithmetic:
Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website!
.
Matthias and Klara live in a high-rise building. Klara lives 12 floors above Matthias.
One day, Matthias climbs the staircase to visit Klara.
When the amount of floors he has traveled equals the number of remaining floors, he is on the 8th floor.
On which floor does Klara live ?
~~~~~~~~~~~~~~~~~~~~~~~~~~

Mental solution When Matthias was on 8-th floor, the number of the remaining floors to climb was 12/2 = 6, according to the condition. Hence, Klara lives on the 8+6 = 14 (fourteenth) floor. ANSWER. Klara lives on the 14-th floor. CHECK. Then Matthias lives at the 14-12 = 2 (second) floors. 14-8 = 6 floors to climb, and 8-2 = 6 floors to climb, which is consistent with the problem's description.

Solved mentally.

This simple primitive problem does not require any more complicated technique.

===============================================================================

This problem is really simple and primitive (at the level of the 3-rd grade),
but it teaches to read the problem attentively to understand its meaning in full.

It also develops the student's common sense and teaches a student to think
independently and to organize his or her thoughts to express the solution
in simple and clear manner. So, although the problem is simple, it has a significant educational value.

I think that if a student will solve, let say, 10 (ten) Math problems of this kind on his/her own
in his/her 3rd grade, it would create a good mental charge for his/her mind for all the following years.

The problems of this kind are real treasures for the young mind.

Answer by josgarithmetic(39616)   (Show Source):
You can put this solution on YOUR website!

m climbs some floors.
x, number of floors climbed on the way
, number of remaining floors to travel when traveled x floors

he started at level m and traveled x floors up, and is at floor 8.

Not finishe but enough to solve.

--
No something's wrong in the above work.

Question 1166599: You have $500,000 saved for retirement. Your account earns 3% interest.
How much will you be able to pull out each month, if you want to be able to take withdrawals for 25 years?
Round your answer to the nearest dollar.
$____
Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website!
.
You have $500,000 saved for retirement. Your account earns 3% interest.
How much will you be able to pull out each month, if you want to be able to take withdrawals for 25 years?
Round your answer to the nearest dollar.
~~~~~~~~~~~~~~~~~~~~~~

            This problem in the post is posed INCORRECTLY and UNPROFESSIONALLY.

To be correct, the problem should describe

        (a)   how often the account is compounded,

    and

        (b)   when the withdrawals are made - at the beginning or at the end of each month.

Question 1172923: Compute the median and mode of the following distribution
Marks 10-19 20-29 30-39 40-49 50-59
No. of students 5 25 40 20 10
Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website!
**1. Median**
* **Find the cumulative frequency:**
* 10-19: 5
* 20-29: 5 + 25 = 30
* 30-39: 30 + 40 = 70
* 40-49: 70 + 20 = 90
* 50-59: 90 + 10 = 100
* **Identify the median class:**
* The total number of students is 100.
* The median is the value that divides the data into two equal halves, so we need the 50th value.
* The cumulative frequency that includes the 50th value is 70, which corresponds to the 30-39 class.
* **Calculate the median:**
* Median = L + [(N/2 - CF) / f] * h
* L = lower limit of the median class = 30
* N = total number of students = 100
* CF = cumulative frequency of the class before the median class = 30
* f = frequency of the median class = 40
* h = class width = 10
* Median = 30 + [(100/2 - 30) / 40] * 10
* Median = 30 + (20/40) * 10
* Median = 30 + 5
* **Median = 35**
**2. Mode**
* **Identify the modal class:**
* The modal class is the class with the highest frequency.
* In this case, the modal class is 30-39 with a frequency of 40.
* **Calculate the mode:**
* Mode = L + [(f1 - f0) / (2f1 - f0 - f2)] * h
* L = lower limit of the modal class = 30
* f1 = frequency of the modal class = 40
* f0 = frequency of the class before the modal class = 25
* f2 = frequency of the class after the modal class = 20
* h = class width = 10
* Mode = 30 + [(40 - 25) / (2 * 40 - 25 - 20)] * 10
* Mode = 30 + (15 / 35) * 10
* Mode = 30 + 4.29
* **Mode = 34.29**
**Therefore:**
* **Median = 35**
* **Mode = 34.29**

Question 1179470: Sam owns a triangular piece of land on which the taxcollector wishes to determine the correctproperty tax. Sam tells the collector that “the firstside lies on a straight section of road and the secondside is a stone wall. The wall meets the road at a24-degree angle. The third side of the property isformed by a 180-foot-long fence, which meets the wallat a point that is 340 feet from the corner wherethe wall meets the road.” After a little thought,the tax collector realizes that Sam’s descriptionof hisproperty is ambiguous, because there are still twopossible lengths for the first side. By means ofa cleardiagram, explain this situation, and calculate thetwo possible areas, to the nearest square foot.
Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website!
Here's a diagram that explains the ambiguous case and the calculations for the two possible areas of Sam's triangular piece of land.
**Diagram:**
[asy]
unitsize(0.8 cm);
pair A, B, C, D;
A = (0,5);
B = (0,0);
C = (8,0);
D = (8,3);
draw(A--B--C--cycle);
draw(C--D);
label("$A$", A, N);
label("$B$", B, SW);
label("$C$", C, SE);
label("$D$", D, NE);
label("$24^\circ$", B + (0.8,0.2));
label("$180$", (A + C)/2, NE);
label("$340$", (C + D)/2, NE);
[/asy]
Let:
* AB be the first side (road)
* BC be the second side (wall)
* AC be the third side (fence)
* D be the point where the fence meets the wall
We are given:
* Angle ABC = 24°
* AC = 180 feet
* CD = 340 feet
**Ambiguity:**
The ambiguity arises because we are not given which side of the wall the fence lies on. This leads to two possible triangles:
* **Triangle ABC:** The fence lies on the same side of the wall as the road.
* **Triangle ABD:** The fence lies on the opposite side of the wall as the road.
**Calculations:**
**Triangle ABC:**
1. **Find angle ACB:**
Using the Law of Sines in triangle ACD:
```
sin(∠ACD) / AC = sin(∠CAD) / CD
sin(∠ACD) / 180 = sin(24°) / 340
sin(∠ACD) ≈ 0.214
∠ACD ≈ 12.4°
```
Since ∠ACD and ∠ACB are supplementary angles:
```
∠ACB ≈ 180° - 12.4° = 167.6°
```
2. **Find angle BAC:**
```
∠BAC ≈ 180° - ∠ABC - ∠ACB
∠BAC ≈ 180° - 24° - 167.6° = -11.6°
```
Since angles cannot be negative, this triangle is not possible.
**Triangle ABD:**
1. **Find angle ADB:**
Using the Law of Sines in triangle ACD:
```
sin(∠ADB) / AC = sin(∠CAD) / CD
sin(∠ADB) / 180 = sin(24°) / 340
sin(∠ADB) ≈ 0.214
∠ADB ≈ 12.4°
```
2. **Find angle BAD:**
```
∠BAD ≈ 180° - ∠ABD - ∠ADB
∠BAD ≈ 180° - 24° - 12.4° = 143.6°
```
3. **Find AD:**
Using the Law of Sines in triangle ABD:
```
AD / sin(∠ABD) = BD / sin(∠BAD)
AD / sin(24°) = 340 / sin(143.6°)
AD ≈ 224.3 \text{ feet}
```
4. **Find AB:**
Using the Law of Cosines in triangle ABD:
```
AB^2 = AD^2 + BD^2 - 2 * AD * BD * cos(∠ADB)
AB^2 ≈ 224.3^2 + 340^2 - 2 * 224.3 * 340 * cos(12.4°)
AB ≈ 129.4 \text{ feet}
```
5. **Calculate the area:**
Using Heron's formula with sides AB, BD, and AD:
```
s = (AB + BD + AD) / 2 ≈ (129.4 + 340 + 224.3) / 2 ≈ 346.85
Area ≈ √[s(s - AB)(s - BD)(s - AD)]
Area ≈ √[346.85(346.85 - 129.4)(346.85 - 340)(346.85 - 224.3)]
Area ≈ 14595 \text{ square feet}
```
**Conclusion:**
The two possible lengths for the first side are approximately 129.4 feet. The area of the triangular piece of land is approximately 14595 square feet.

Question 1184365: In January of 2017, you planted a rare variety of tomato. In 2 month time, you recorded the number of tomatoes harvested every week from various plots. Your data contained

140, 140, 100, 120, 110, 130, 110, 110, 140, 100, 130, 80.

A. Find the mean, mode, median and range for your data set of number of tomatoes. B. If the number of tomatoes doubles each week in the year 2017, what will be the mean, mode, median and range for the 2017 data? C. If, instead, there are five more tomatoes per week in the year 2017, what will be the mean, mode, median and range for the 2017 data?
Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website!
Here's the analysis of your tomato harvest data:
**A. Original Data Analysis:**
* **Mean:** (140 + 140 + 100 + 120 + 110 + 130 + 110 + 110 + 140 + 100 + 130 + 80) / 12 = 120 tomatoes
* **Mode:** 110 and 140 (both appear 3 times)
* **Median:** First, order the data: 80, 100, 100, 110, 110, 110, 120, 130, 130, 140, 140, 140. The median is the average of the two middle numbers: (110 + 120) / 2 = 115 tomatoes
* **Range:** 140 (highest) - 80 (lowest) = 60 tomatoes
**B. Doubling Each Week:**
If the number of tomatoes doubles each week, we multiply each data point by 2:
280, 280, 200, 240, 220, 260, 220, 220, 280, 200, 260, 160
* **Mean:** (280 + 280 + 200 + 240 + 220 + 260 + 220 + 220 + 280 + 200 + 260 + 160) / 12 = 240 tomatoes (the mean also doubles)
* **Mode:** 220 and 280 (both appear 3 times)
* **Median:** Order the data: 160, 200, 200, 220, 220, 220, 240, 260, 260, 280, 280, 280. Median: (220 + 240) / 2 = 230 tomatoes
* **Range:** 280 - 160 = 120 tomatoes (the range also doubles)
**C. Five More Tomatoes Each Week:**
If there are five more tomatoes each week, we add 5 to each data point:
145, 145, 105, 125, 115, 135, 115, 115, 145, 105, 135, 85
* **Mean:** (145 + 145 + 105 + 125 + 115 + 135 + 115 + 115 + 145 + 105 + 135 + 85) / 12 = 125 tomatoes (the mean increases by 5)
* **Mode:** 115 and 145 (both appear 3 times)
* **Median:** Order the data: 85, 105, 105, 115, 115, 115, 125, 135, 135, 145, 145, 145. Median: (115 + 125) / 2 = 120 tomatoes
* **Range:** 145 - 85 = 60 tomatoes (the range stays the same)
**Key Observations:**
* When the data is scaled (multiplied by 2), the mean, mode, median, and range all scale by the same factor.
* When a constant is added to the data, the mean, mode, and median increase by that constant, but the range remains unchanged.

Question 1186499: The safe load LF a wooden beams to put it up both and varies jointly as the wet W in the square of the deputy and inversely as the length , l . a wooden beams 7 inches wide 9 inches deep and 7 feet long holds up 39701 pounds what load will they be 9 inches wide 6 inches deep and 18 foot long of the same material support round your answer to the nearest integer if necessary
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13198)   (Show Source):
You can put this solution on YOUR website!

When you post a problem, politeness should be shown if you want someone to respond. You are not posting a message to a friend on your favorite social messaging network.

Type your message using proper English, including punctuation. And READ what you are posting before you post it.

In this problem, the maximum load varies directly as the width w, directly as the square of the depth d, and inversely as the length l. The given information is that the maximum load is 39701 pounds when the width is 7 inches, the depth is 9 inches, and the length is 7 feet. We are asked to find the maximum load when the width is 9 inches, the depth is 6 inches, and the length is 18 feet.

One way to solve the problem is to use the variation formula with the given set of data to find the constant of proportionality using the given information, then use that constant with the new set of data to find the new safe load.

But since we are only asked to find the safe load for one other set of data, we don't need to do that much work. Instead, we can just determine how the maximum load changes for the change in each of the parameters.

The width changes from 7 to 9 inches. Since the safe load varies directly with the width, this changes the safe load by a factor of (9/7).
The depth changes from 9 to 6 inches. Since the safe load varies directly as the square of the depth, this changes the safe load by a factor of (6/9)^2.
The length changes from 7 feet to 18 feet. Since the safe load varies inversely as the length, this changes the safe load by a factor of (7/18).

So the safe load with the new parameters is

= 8822.4444...

Rounded to the nearest integer, the new safe load is

ANSWER: 8822 pounds

Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website!
.

Soup of words.

Question 1209513: Emily earns $7.50 per hour. How much does she earn in in 3 hours?
Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website!
.
Emily earns $7.50 per hour. How much does she earn in 3 hours?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

She will earn $7.50 + $7.50 + $7.50 = $22.50 = 3 * $7.50.

Question 1197912: The heights of adult men in America are normally distributed, with a mean of 69.3 inches and a standard deviation of 2.68 inches. The heights of adult women in America are also normally distributed, but with a mean of 64.5 inches and a standard deviation of 2.59 inches.
a) If a man is 6 feet 3 inches tall, what is his z-score (to two decimal places)?
z =

b) If a woman is 5 feet 11 inches tall, what is her z-score (to two decimal places)?
z =

c) Who is relatively taller?
-The 5 foot 11 inch American woman
-The 6 foot 3 inch American man
Answer by onyulee(41)   (Show Source):
You can put this solution on YOUR website!
**a) Z-score for the 6-foot-3-inch man:**
* **Convert height to inches:** 6 feet 3 inches = 75 inches
* **Calculate z-score:**
z = (x - μ) / σ
z = (75 - 69.3) / 2.68
z ≈ 2.14
**b) Z-score for the 5-foot-11-inch woman:**
* **Convert height to inches:** 5 feet 11 inches = 71 inches
* **Calculate z-score:**
z = (x - μ) / σ
z = (71 - 64.5) / 2.59
z ≈ 2.51
**c) Who is relatively taller?**
* The **woman** is relatively taller.
**Explanation:**
* A higher z-score indicates that the individual is further above the mean of their respective population.
* The woman's z-score of 2.51 is higher than the man's z-score of 2.14, meaning she is further above the average height for women than the man is above the average height for men.

Question 1208706: 1/2 * [2/3 - 5/6 * (3/4)]

Answer by jhunjiro(67)   (Show Source):
You can put this solution on YOUR website!
- multiply (5/6)*(3/4)
- subtract (2/3)-(15/24) note: 2/3 = 16/24

multiply (1/2)*(1/24)
Final Answer:

Question 1208136: If a student scores 85,79,92, and 100 on her math quizzes then what was her average grade?

Found 2 solutions by greenestamps, josgarithmetic:
Answer by greenestamps(13198)   (Show Source):
You can put this solution on YOUR website!

By the basic method, using the definition of average directly....

ANSWER: 89

Or by a method which is sometimes easier in cases where all the numbers are "close together"....

(1) Using a quick examination of the given numbers, make a guess for the average. In this example, 90 should be close.

(2) Determine, for each given number, the "over" or "under" compared to your guess for the average; then find the total over or under.
85: -5
79: -11
92: +2
100: +10
total: -16+12 = -4

(3) Divide the total over or under by the number of quiz scores to find the average over or under
-4/4 = -1

Adjust your guess by that average over or under to get the actual average
90+(-1) = 89

ANSWER (again, of course): 89

Answer by josgarithmetic(39616)   (Show Source):
You can put this solution on YOUR website!
The sum, divided by how many of them

something still missing.
Given scores, but want grade - missing too much in between

Question 1208044: Given f(x) = -4x + 1,

A. Find the average rate of change from 2 to 5.

B. Find an equation of the secant line containing (2, f(2)) and (5, f(5)).

Found 3 solutions by math_tutor2020, Edwin McCravy, AnlytcPhil:
Answer by math_tutor2020(3816)   (Show Source):
You can put this solution on YOUR website!

f(x) is linear since it fits the y = mx+b format
m = -4 = slope
b = 1 = y intercept

The slope is the same as the rate of change.
This is because,
slope = rise/run = (change in y)/(change in x)

Therefore the answer to part A is -4.
The "from 2 to 5" portion won't affect the answer.
The rate of change from p to q will also be -4.
The slope is the same throughout the line.

The answer to part B is the equation y = -4x+1
The secant line is identical to the original line itself.
It's only when you have curves like parabolas when the secant line is different from the function curve.

Answer by Edwin McCravy(20054)   (Show Source):
You can put this solution on YOUR website!
Given f(x) = -4x + 1,
A. Find the average rate of change from 2 to 5.
As x goes from 2 to 5, y [or f(x)] goes from f(2)=-4(2)+1=-7 to f(5)=-4(5)+1=-19 From -7 to -19 is a change of (-19)-(-7)=-19+7=-12 in y From 2 to 5 is a change of 5-2 = +3 in x So the average change in y [or f(x)] per the average change in x is -12 units change in y per a +3 change in x, which means an average change of (-12)/(+3)=-4 y-units change per x-units change. That's what the slope is, the change in y, divided by the change in x Answer: -4 change in f(x) y-units per x-unit change.
B. Find an equation of the secant line containing (2, f(2)) and (5, f(5)).
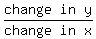
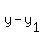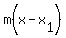
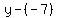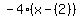
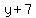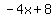
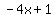change y to f(x) 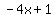So the secant line coincides with the graph of f(x). [That happens when the graph of the given function f(x), is a line, but not when the given function curves]. Here is a case when the given function f(x) curves, and the secant line does not coincide with the given function f(x) The black line is the secant line. It only has two points in common with the function f(x) (the red curve). But your problem here is not a curve: The case you were given was a special case when the secant line happens to coincide with the function f(x), like what you see below, where the black line, which is the secant line, coincides with the red line, which is the graph of f(x). Your teacher gave you a very special case, but most graphs for f(x) are not straight lines, and the secant lines will usually have only two points in common with the graph of the given function f(x) like the graph above. Remember what the word "secant" means, a line that cuts through a curve, as you see in the first curve. [Remember from your geometry that a secant line was a line that cuts through a circle.] Your problem here is a special case when the secant line doesn't "cut through" the curve of f(x) but coincides with it. This type problem is to prepare you for calculus, where you will learn about the secant line approaching a tangent line. You will also remember from your geometry that a tangent line just touches a circle in one point, and does not cut through the circle. I didn't want you to get confused because your teacher gave you such a special case. Just remember that most of your problems will be like the curve in the first graph above, not the lower special case, which you were given. Edwin

Answer by AnlytcPhil(1806)   (Show Source):
You can put this solution on YOUR website!

Question 1207848: The length of a rectangle is 5 feet more than three times the width. The perimeter of the rectangle is 146 feet. What is the width and the length of the rectangle? State what x represents, state the equation, and then state the answer.
Found 3 solutions by ikleyn, Edwin McCravy, josgarithmetic:
Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website!
.
The length of a rectangle is 5 feet more than three times the width.
The perimeter of the rectangle is 146 feet. What is the width and the length of the rectangle?
State what x represents, state the equation, and then state the answer.
~~~~~~~~~~~~~~~~~~

        As I interpret the problem and the question/request, this visitor
        (or a person of whom he/she does represent) wants that we, the tutors,
        perform/share a standard mantra which should be played/pronounced as a solution.

        As he/she mentions only one unknown x, it means the solution be presented in one unknown.

        Such solution is presented below. It is one of possible mantra.

Let x be the width of the rectangle, in feet. Then the length of the rectangle is 3x+5 feet, according to the problem. For the perimeter of the rectangle, we can write this equation x + (3x+5) + x + (3x+5) = 146. It reflects the fact that the perimeter of a rectangle is the sum of the lengths of all four its sides. Simplify and find x 8x + 10 = 146, 8x = 146 - 10, 8x = 136 x = 136/8 = 17. Thus the width is 17 feet; the length is 3*17+5 = 56 feet. ANSWER. The width is 17 feet; the length is 56 feet. CHECK. The perimeter is 17 + 56 + 17 + 56 = 146 feet. ! correct !

At this point, the problem is solved in full with all necessary explanations,
with complete checking and precisely in the form as requested.

Now the visitor can use this my post as a TEMPLATE to solve thousand
other similar problems or as a standard mantra to teach others from a pulpit
(which is of this visitor the most deepest desire).

Answer by Edwin McCravy(20054)   (Show Source):
You can put this solution on YOUR website!

You can also solve this system by substitution: If you must use an x, change either L or W to x and state whether it was the length or width you chose x to represent. Edwin

Answer by josgarithmetic(39616)   (Show Source):
You can put this solution on YOUR website!
-----------------------------------------
What is the width and the length of the rectangle? State what x represents, state the equation, and then state the answer.
-----------------------------------------

No instructions for what to do with "x".

----------------------------------------------
The length of a rectangle is 5 feet more than three times the width. The perimeter of the rectangle is 146 feet. What is the width and the length of th......
---------------------------------------------

-------------You KNOW what is w in here. Solve....

Question 1206863: You invested $24 comma 00024,000 in two accounts paying 5 %5% and 7 %7% annual interest, respectively. If the total interest earned for the year was $1400, how much was invested at each rate?
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13198)   (Show Source):
You can put this solution on YOUR website!

The response from the other tutor shows a typical formal algebraic solution.

The discussion below shows a less formal process for solving any 2-part mixture problems like this.

The idea behind this method is that the ratio between the amounts invested in the two accounts is exactly determined by where the overall percentage return lies between the percentages of the two accounts.

$24,000 all invested at 5% would earn $1200 interest; all invested at 7% would earn $1680 interest.

Picture the three interest amounts -- $1200, $1400, and $1680 -- on a number line and observe/calculate that $1400 is (1400-1200)/(1680-1200) = 200/480 = 5/12 of the way from $1200 to $1680.

That means 5/12 of the total was invested at the higher rate.

5/12 of $24,000 is $10,000. So $10,000 was invested at 7% and the other $14,000 at 5%.

ANSWER: $10,000 at 7%; $14,000 at 5%

CHECK: .07(10000)+.05(14000) = 700+700 = 1400

Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website!
.
You invested $24 comma 00024,000 in two accounts paying 5 %5% and 7 %7% annual interest, respectively.
If the total interest earned for the year was $1400, how much was invested at each rate?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Let x dollars be the amount invested at 7%. then the amount invested at 5% is (24000-x) dollars. Write equation for the total annual interest 0.07x + 0.05*(24000-x) = 1400 dollars. Simplify and find x 0.07x + 0.05*24000 - 0.05x = 1400 0.07x - 0.05x = 1400 - 0.05*24000 0.02x = 200 x = 200/0.02 = 20000/2 = 10000. ANSWER. $10000 invested at 7%, the rest, or 24000-10000 = 14000 dollars invested at 5%. CHECK. 0.07*10000 + 0.05*14000 = 1400 dollars, the combined annual interest. ! correct !

Solved.

Question 1205920: A ball is thrown upward from the top of a building 80 feet tall with an initial velocity of 64 feet per second. Solve the equation: -16t^2+64t+80=144 to find the time t (in seconds) at which the ball is 144 feet from the ground.
Answer by ankor@dixie-net.com(22740)   (Show Source):
You can put this solution on YOUR website!
A ball is thrown upward from the top of a building 80 feet tall with an initial velocity of 64 feet per second.
Solve the equation: -16t^2+64t+80=144 to find the time t (in seconds) at which the ball is 144 feet from the ground.
:
-16t^2 + 64t + 80 = 144
Simplify, divide equation by -16
t^2 - 4t - 5 = -9
t^2 - 4t - 5 + 9 = 0
t^2 - 4t + 4 = 0
Factors to
(t-2)(t-2) = 0
t = 2 Seconds

Question 1205910: It takes 3 people 4 days to build a garage.
A) How long does it take one person to build the garage?
B)How long does it take four people to build the garage?
C)How many people are needed to build the garage in 2 days?
Found 3 solutions by greenestamps, josgarithmetic, ikleyn:
Answer by greenestamps(13198)   (Show Source):
You can put this solution on YOUR website!

The other tutor shows one common method for answering the questions by finding the total number of man-days it takes to build the garage.

A different way for solving problems like this is to look at how each change in the numbers affects the other numbers.

We are given that it takes 3 people 4 days to build the garage. Using that information....

A) How long does it take one person to build the garage?
1/3 as many workers means 3 times as many days. ANSWER: 4*3 = 12

B) How long does it take four people to build the garage?
4/3 as many workers means 3/4 as many days. ANSWER: (3/4)*4 = 3

C) How many people are needed to build the garage in 2 days?
Half as many days means twice as many workers. ANSWER: 3*2 = 6

Answer by josgarithmetic(39616)   (Show Source):
You can put this solution on YOUR website!
r, the work rate for 1 person

If one job is "build a garage", the description is .
This means, or one person needs 12 days to build a garage.

How much time for 4 people?

-----three days

How many workers to do the job in 2 days?
n workers

Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website!
.
It takes 3 people 4 days to build a garage.
A) How long does it take one person to build the garage?
B)How long does it take four people to build the garage?
C)How many people are needed to build the garage in 2 days?
~~~~~~~~~~~~~~~~~~~

The entire job is 3*4 = 12 man-days. From here (a) one person will complete this job in 12:1 = 12 days; (b) four persons will complete this job in 12:4 = 3 days; (c) to make this job in 2 days, 12:2 = 6 persons are needed.

That's all.

-------------------

To see many other similar (and different) problems, solved by the same method, look into the lesson
    - Rate of work problems
in this site.

It was written specially for you, to make your horizon WIDER.

Consider this lesson as your textbook, handbook, guide, tutorials and (free of charge) home teacher.

Be trained in solving rate of work problems.

Come again to this forum soon to learn something new ( ! )

Question 1205795: What is the median of 80,80,80,80,80,85,85,85,85,85,90,90,90,90,90

Found 3 solutions by greenestamps, math_tutor2020, MathLover1:
Answer by greenestamps(13198)   (Show Source):
You can put this solution on YOUR website!

You don't need to go into much detail to answer the question if you know what "median" means.

The set of data consists of 5 each of 3 distinct values, so there are equal numbers of values above and below the middle value. That means the median is the middle value.

ANSWER: 85

Answer by math_tutor2020(3816)   (Show Source):
You can put this solution on YOUR website!

Answer: 85

==========================================================================

Explanation

Method 1

The first task is to sort the values. Thankfully that has already been done for us.
Always make sure the values are sorted before attempting to find the median.

The original string of values
80,80,80,80,80,85,85,85,85,85,90,90,90,90,90
rewrites to
80,80,80,80,80,
85,85,85,85,85,
90,90,90,90,90
which I think is easier to see how many items there are. This block of values is 3 items tall and 5 items across. There are 3*5 = 15 values total.

n = 15 is the sample size.
n/2 = 15/2 = 7.5 which rounds to 8
The median is in slot 8
7 values are below it, and 7 values are above it
7+1+7 = 15 values total

The value in slot 8 is 85. It's the 3rd copy of "85" in the second row of this block:
80,80,80,80,80,
85,85,85,85,85,
90,90,90,90,90
Or you can return back to the original string of values to count out 8 positions from the left.

--------------------------------------------------------------------------

Method 2

Chop off the first and last values of
80,80,80,80,80,85,85,85,85,85,90,90,90,90,90
to get
80,80,80,80,80,85,85,85,85,85,90,90,90,90,90
which cleans up to
80,80,80,80,85,85,85,85,85,90,90,90,90

Repeat the process again to go from
80,80,80,80,85,85,85,85,85,90,90,90,90
to
80,80,80,85,85,85,85,85,90,90,90

Keep this process going until either (a) we end up with one value or (b) we end up with 2 values
80,80,80,85,85,85,85,85,90,90,90
80,80,85,85,85,85,85,90,90
80,85,85,85,85,85,90
85,85,85,85,85
85,85,85
85
We see that 85 is the middle most value.

Or what we can do is cross off say 3 items at a time from each endpoint.
This is to help speed things up.
80,80,80,80,80,85,85,85,85,85,90,90,90,90,90
~~80,80,80~~,80,80,85,85,85,85,85,90,90,~~90,90,90~~
80,80,85,85,85,85,85,90,90
~~80,80,85~~,85,85,85,~~85,90,90~~
85,85,85

Note: If you end up with 2 values tied for the middle, then take the midpoint of them. This occurs only when the sample size is an even number.
The midpoint formula is (p+q)/2 where p and q are the middle most values.

--------------------------------------------------------------------------

Method 3

Use software such as a speadsheet or online calculator.
This method doesn't have much to explain about it, other than it's something I only recommend as a way to check your answer.
It's best to know how to find the median by hand.

Answer by MathLover1(20849)   (Show Source):
You can put this solution on YOUR website!

80,80,80,80,80,85,85,||,85,85,90,90,90,90,90
the median is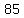

Question 1205235: The average rainfall in Waterloo has increased at an annual rate of 2%. If the total rain fall was 856mm in 2002. What is the expected rainfall in 2005? (mm)
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website!
856 * 1.02 ^ (2005 - 2002) = 856 * 1.02 ^ 3 = 908.394048.
the expected rainfall in 2005 is 908.394048mm.

Question 1205142: How can I multiply a inverse function by an other inverse function

Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website!
the same way you would multiply any equation by any equation.
for example:
equation 1 is y = x^2
equation 2 is y = x^3
inverse equation 1 is y = x^(1/2)
inverse equation 2 is y = x^(1/3)
inverse equation 1 by inverse equation 2 to get y = x^(1/2) * x^(1/3) = x^(1/6)
it looks like if you multiply the original equations by each other you would get y = x^6 and the inverse equation to that is y = x^(1/6).

so, i would say, you can probably do it 2 ways.
1.
multiply the inverse equations by each other as you would multiply any equation by each other.
2.
multiply the original equations by each other and then get the inverse of that.
if option 2 is true, then you can check that you did the multiplication correctly by doing it both ways and compare your answer to see if they are the same.

try it out and let me know how you do.
send me the original equations and the inverse equation as well and i'll give it a shot from this end.

Question 1204991: A teacher wants to calculate the average score of her students. She has the scores of 20 students, but she accidentally misplaced one score. If the average of the remaining 19 scores is 85, what should be the misplaced score to maintain a weighted mean of 87?
Found 3 solutions by greenestamps, mananth, josgarithmetic:
Answer by greenestamps(13198)   (Show Source):
You can put this solution on YOUR website!

A quick informal solution using logical reasoning, if formal algebra is not required.

The 19 scores she has are, on average, 87-85 = 2 points short of the desired mean; so together they are 19*2 = 38 points short. That means the missing score must be 38 points above the desired mean.

ANSWER: 87+38 = 125

Answer by mananth(16946)   (Show Source):
You can put this solution on YOUR website!
A teacher wants to calculate the average score of her students. She has the scores of 20 students, but she accidentally misplaced one score. If the average of the remaining 19 scores is 85, what should be the misplaced score to maintain a weighted mean of 87?
The average of the 19 students is 85 as calculated by teacher
So total score = 19*85 =1615
Let the misplace score be x
Total score of 20 students will be 1615+x
The average is 87
The average now is (1615+x)/20= 87
1615+x = 87*20
1615+x= 1740
x = 1740-1615
x =125

The misplaced score is 125 to maintain a mean of 87.
CHECK
1615+125 =1740
1740/20=87

Answer by josgarithmetic(39616)   (Show Source):
You can put this solution on YOUR website!
125

Teacher forgot to use some x.
19 students had average of 85 but for all 20 students, the real average was 87.

Question 1204908: In a recent survey of 1124 students, 980 of them would like to recommend www.helpyourmath.com to their friends. Construct a 90% confidence interval to estimate the proportion of all students who would recommend www.helpyourmath.com to their friends.
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website!
the mean proportion is p = 980/1124 = .871886121.
q = 1-p = .128113879.
the standard error is sqrt(p * q / 1124) = sqrt(.871886121*.12811387/1124) = .0099688444.

the two tailed 90% confidence interval requires a z-score of plus or minus 1.645.

the z-score formula used is z = (x - m) / s
z is the z-score
x is the desired proportion.
m is the mean proportion.
s is the standard error.

to find the lower desired proportion, the formula becomes:
-1.645 = (x - .871886121) / .009968844.
solve for x to get x = -1.645 * .009968844 + .871886121 = .855487372.
to find the upper desired proportion, the formula becomes:
1.645 = (x - .871886121) / .009968844.
solve for x to get x = 1.645 * .009968844 + .i71886121 = .88828487.

round to 3 decimal places to get 90% confidence interval is from .855 to .888.

since the value is n * p, you get:

mean is 1124 * 980 / 1124 = 980
low threshold is 1124 * .855 = 961 roughly.
high threshold is 1124 * .888 = 998 roughly.

your solution should be that the 90% confidence interval of the proportion is .855487372 to.88828487.
round your numbers as required.

Question 1204722: True or false: The standard deviation of {7,7,7,7} is 7
Answer by math_tutor2020(3816)   (Show Source):
You can put this solution on YOUR website!

Normally your teacher should specify if referring to population vs sample standard deviation. However, in this case, both are the same value. Both are zero.

The standard deviation measures how spread out a set is.
The smallest it can get is 0 which only happens when all values of the set are the same.
Therefore, the standard deviation (both versions) of {7,7,7,7} is 0.

Answer: False

Question 1204664: a nurse wants to make 50 ml of a 20% morphine solution. she needs to mix 10% morphine solution with 50% morphine solution to make this happen. how many ml of each must she mix?
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3816)   (Show Source):
You can put this solution on YOUR website!

Batch A: 10% morphine
Batch B: 50% morphine
Target concentration: 20% morphine

The gap from 10% to 20% is 10
The gap from 20% to 50% is 30
The ratio 10:30 reduces to 1:3

The nurse will need 3 times as much of one solution compared to the other.
The ratio 1:3 scales up to 1x:3x for some positive real number x.
Add up those parts and set the sum equal to the goal of 50 mL.
1x+3x = 50
4x = 50
x = 50/4
x = 12.5

She'll need x = 12.5 mL of one batch and 3x = 3*12.5 = 37.5 mL of the other batch.

The question is: which values go where?

Let's make a table where we have 12.5 mL of batch A and 37.5 mL of batch B

Amount of solution Amount of pure morphine
A 12.5 0.10*12.5 = 1.25
B 37.5 0.50*37.5 = 18.75
Total 50 1.25+18.75 = 20

The takeaway from that table is we have 20 mL of pure morphine out of 50 mL total
20/50 = 0.40 = 40% is the final concentration.

We wanted a 20% concentration instead, so we must flip the values.

Amount of solution Amount of pure morphine
A 37.5 0.10*37.5 = 3.75
B 12.5 0.50*12.5 = 6.25
Total 50 3.75+6.25 = 10

10 mL of pure morphine out of 50 mL total
10/50 = 0.20 = 20% is the final concentration, which is the target we're after.

Answers:
37.5 mL of the 10% solution
12.5 mL of the 50% solution

More practice with a similar question
https://www.algebra.com/algebra/homework/word/mixtures/Mixture_Word_Problems.faq.question.1204463.html

Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website!
.
a nurse wants to make 50 ml of a 20% morphine solution.
she needs to mix 10% morphine solution with 50% morphine solution to make this happen.
how many ml of each must she mix?
~~~~~~~~~~~~~~~~~~~

Let x be the the volume of the 50% morphine solution to use, in milliliters. Then the volume of the 10% solutions of morphine is (50-x) mL, to make the total volume of 50 mL. The 50% solution contributes 0.5x mL of the pure morphine to the final mixture. The 10% solution contributes 0.1*(50-x) mL of the pure morphine to the final mixture. So, the total amount of the pure morphine in 50 Ml of the final mixture is 0.5x + 0.1*(50-x) milliliters. We want this amount of the pure morphine provides 20% final solution. So, we write this equation, which describes it 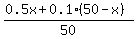= 0.2. Simplify it by multiplying both sides by 50 0.5x + 0.1*(50-x) = 0.2*50. Simplify further and express x 0.5x + 5 - 0.1x = 10 0.5x - 0.1x = 10 - 5 0.4x = 5 x = 5/0.4 = 12.5. ANSWER. 12.5 mL of the 50% morphine solution and 50-12.5 = 37.5 ml of the 10% morhine solution should be used. CHECK. 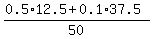= 0.2, or 20% concentration of the final solution. ! correct !

Solved.

-----------------

It is a standard and typical mixture problem.

For introductory lessons covering various types of mixture word problems see
    - Mixture problems
    - More Mixture problems
    - Solving typical word problems on mixtures for solutions
    - Typical word problems on mixtures from the archive
in this site.

You will find there ALL TYPICAL mixture problems with different methods of solutions,
explained at different levels of detalization, from very detailed to very short.

Read them and become an expert in solution mixture word problems.