if you use the normal distribution tables, you will need to the find the area to the left of the indicated z-score.
that's just the way the tables work.
i used a calculator, because the calculator is more accurate, but i made sure the z-score found was rounded to 3 decimal places before looking for the raw score.
the calculator makes the job easier because you don't have to manually interpolate to find the answer you are looking for.
to show you what's happening, the calculator i used can be found at http://davidmlane.com/hyperstat/z_table.html
while the calculator can find the answer more directly, i used the same method you would use if you were looking into the z-score tables.
your problem states:
On an examination the average grade was 74 and the standard deviation was 7. If 12% of the class are given A's and 30% of the class given B's if the grades are curved to follow a normal distribution,
a)What is the lowest possible A's Marks.
b)What is the highest and lowest possible B's Marks.
Answers:
a)83 marks
b)82 and 75 marks.
you'll be looking for the z-score first and then translating to the raw score.
the calculator can work directly from the raw scores but we won't do that because the tables work from z-scores only.
we'll do the A scorers first.
since A is the highest score and 12% of the class gets an A, then 88% of the class doesn't get an A.
you want to find the z-score that has an area of .88 to the left of it.
that z-score is 1.175 rounded to 3 decimal places.
here's the results of using the online calculator.
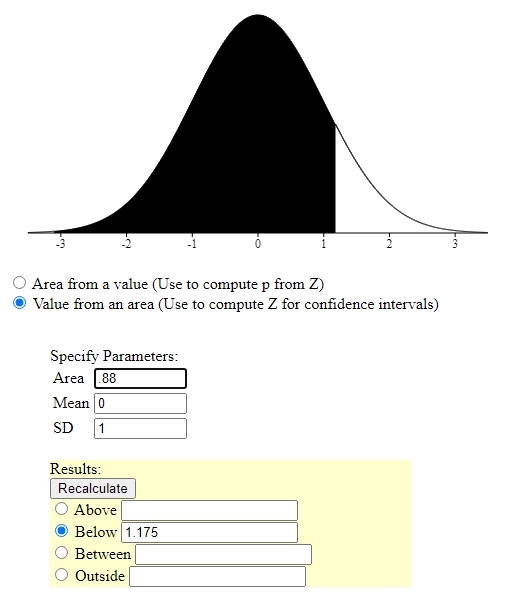
to find the equivalent raw score, you would use the z-score formula of:
z = (x - m) / s
z is the z-score
x is the raw score
mis the mean
s is the standard deviation.
since your mean is 74 and your standard deviation is 7, you would solve for the raw score as follows:
z-score formula becomes:
1.175 = (x - 74) / 7
solve for x to get:
x = 1.175 * 7 + 74 = 82.225.
round up to the nearest integer to get 83.
we'll do the B scorers next.
the B scorers are below the A scorers and above the rest that aren't A or B.
the highest z-score for the B scorers will be the same as the lowest z-score for the A scorers.
that z-score is 1.175.
the difference here is you'll need to round down rather than up.
since the raw score was found to be 82.225, you will round down to 82.
the lowest z-score for the B scorers will be above 12% + 30% = 42% of the area under the normal distribution curve.
that's equivalent to being above 58% of the area under the normal distribution curve.
you are looking for an area of.58 to the left of the z-score.
you would use the calculator to get a z-score of .202.
here's the results of using the online calculator.

the raw score associated with a z-score of.202 is found using the z-score formula.
the formula of z = (x - m) / s becomes .202 = (x - 74) / 7.
solve for x to get:
x = .202 * 7 + 74 = 75.414.
round that up to 76.
the lowest score for a B scorer is 76 and the highest score for a B scorer is 82.
the answers they have are:
a) = 83
b) = 82 and 75
the answers you have are:
a) = 83
b) = 82 and 76
for the 75 score, i believe they rounded down when they should have rounded up.
that's the difference.
a low score of 75 only has 56% of the area to the left of it.
it's a small error, but it's an error.
it should have had at least 58% of the area to the left of it.
a low score of 76 has 61% to the left of it.
that's above 58% area to the left of it.
looks to me like they rounded correctly at the 88% mark, but botched it at the 58% mark.
for above 88%, they rounded up to 83 and for below 88% they rounded down to 82.
for above 58%, they should have rounded up to 76, but rounded down to 75 instead.
that's my opinion.
take it for what it's worth.
the procedure i used, however, is correct.
here's a picture i drew that will hopefully provide you with a visual of what's going on.

this can be a bit confusing, so if you have any questions, fire away.
theo