SOLUTION: Determine the distance of the line 4x - 3y = -5 from the point (2, 1). Write the numerical value only.
Algebra.Com
Question 1166805: Determine the distance of the line 4x - 3y = -5 from the point (2, 1). Write the numerical value only.
Found 2 solutions by solver91311, Theo:
Answer by solver91311(24713) (Show Source): You can put this solution on YOUR website!
Find the slope of the given line.
Calculate the negative reciprocal of the slope of the given line which is the slope of any line perpendicular to the given line.
Use the slope of the perpendicular and the given point in the Point-Slope form of an equation of a line:
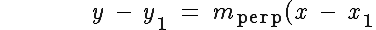)
to derive an equation of the line perpendicular to the given line that passes through the given point.
Solve the 2X2 system of equations consisting of the equation of the given line and the derived equation of the perpendicular line to find the point of intersection of the two lines.
Use the distance formula to calculate the distance from the given point to the point of intersection of the given line and the perpendicular through the given point.
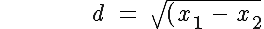^2\ +\ (y_1\,+\,y_2)^2})
John

My calculator said it, I believe it, that settles it

I > Ø

Answer by Theo(13342) (Show Source): You can put this solution on YOUR website!
you want to find the equation of the line perpendicular to the equation of the given line that passes through the point (2,1).
you then want to find the intersection of the given line with the line perpendicular to it.
you'll have two points which you will then want to find the distance between.
the slope of the line perpendicular to the given line is the negative reciprocal of the slope of the given line.
translate the equation of the given line into slope intercept form.
start with 4x - 3y = -5
add 3y to both sides of this equation and add 5 to both sides of this equation to get:
4x + 5 = 3y
this is the same as 3y = 4x + 5.
divide both sides of this equation by 3 to get:
y = 4/3 * x + 5
that's the slope intercept form of the equation for the given line.
the slope of the line perpendicular to it will be the negative reciprocal of 4/3 which is equal to -3/4.
the equation for the line perpendicular to the given line will be y = -3/4 * x + b.
you want to find the value of b.
since the perpendicular line goes through the point (2,1), then replace x with 2 and y with 1 to get 1 = -3/4 * 2 + b
solve for b to get b = 1 + 3/4 * 2.
this makes b = 2.5
the equation of the line perpendicular to the given line becomes:
y = -3/4 * x + 2.5
to find the intersection of the line perpendicular to the given line and the given line, solve those two equations simultaneously.
the two equations are:
y = 4/3 * x + 5 (given line)
y = -3/4 * x + 2.5 (line perpendicular to given line)
subtract the second equation from the first to get:
0 = (4/3 - -(3/4)) * x + 2.5
simplify to get:
0 = (4/3 + 3/4) * x + 2.5
simplify further to get:
0 = 25/12 * x + 2.5
solve for x to get:
x = -2.5 / (25/12) = -1.2
that's the x-value of the intersection point.
the y value can be found by replacing x in either equation with -1.2.
in the equation of y = 4/3 * x + 5, replace x with -1.2 to get y = 3.4
in the equation of y = -3/4 * x + 2.5, replace x with -1.2 to get y = 3.4
the y values are the same because the same point is in both lines.
the intersection point is (-1.2, 3.4)
you now have two point that will allow you to find the distance between them.
the points are (-1.2,3.4) and (2,1).
the distance between them is given by the formula d = sqrt((x2-x1)^2 + (y2-y1)^2).
that becomes d = sqrt((2+1.2)^2 + (1-3.4)^2) = sqrt(16) = 4
that's the distance between the point (2,1) and the given line.
those equations can be graphed as shown below.

RELATED QUESTIONS
Find the exact directed distance from the line 4x+3y=5 to the point (2,-5). (answered by Alan3354)
Find the line which goes through the point (2,-5) and is perpendicular to the line... (answered by josgarithmetic)
Find the line which goes through the point (2,-5) and is perpendicular to the line... (answered by josgarithmetic,ikleyn)
Find the distance from the point (9,5) to the line 4x - 3y =... (answered by khwang)
write an equation in point slope form of the line through the point (-5, 2) to the line... (answered by Fombitz)
Write an equation in point slope form of the line through the point (-5, 2) perpendicular (answered by Fombitz)
determine the shortest distance from the point e(1,-4) to the line through points... (answered by josgarithmetic,mananth,greenestamps)
The magnitude of the distance from the line 5x = By + 26 to the point (3, -5) is 49/13.... (answered by greenestamps,math_helper)
can someone plss help im stuck
1.find the numerical value of 2x-3/x^2-4x+1. when x=-4. (answered by ewatrrr)
