Tutors Answer Your Questions about Central-limit-theorem (FREE)
Question 1165554: lim (x-> -inf) (x^2+4^-x)/(x^2-4^x)
Answer by ikleyn(52779)   (Show Source):
Question 1178703: Use the given degree of confidence and sample data to construct a confidence interval for the population proportion p.
Of 82 adults selected randomly from one town, 66 have health insurance. Find a 90% confidence interval for the true proportion of all adults in the town who have health insurance.
Answer by CPhill(1959)  (Show Source):
You can put this solution on YOUR website! Let's construct the 90% confidence interval for the population proportion.
**1. Define the Variables:**
* **Sample size (n):** 82
* **Number of adults with health insurance (x):** 66
* **Sample proportion (p̂):** x / n = 66 / 82 ≈ 0.8049
* **Confidence level:** 90%
**2. Find the Z-score:**
* For a 90% confidence interval, the z-score (zα/2) is 1.645 (from a z-table or calculator).
**3. Calculate the Standard Error (SE):**
* SE = √[p̂(1 - p̂) / n]
* SE = √[0.8049(1 - 0.8049) / 82]
* SE = √[0.8049(0.1951) / 82]
* SE = √[0.157036 / 82]
* SE = √0.001915073
* SE ≈ 0.04376
**4. Calculate the Margin of Error (ME):**
* ME = zα/2 * SE
* ME = 1.645 * 0.04376
* ME ≈ 0.07198
**5. Calculate the Confidence Interval:**
* Lower Bound: p̂ - ME = 0.8049 - 0.07198 ≈ 0.73292
* Upper Bound: p̂ + ME = 0.8049 + 0.07198 ≈ 0.87688
**6. Express the Confidence Interval:**
* The 90% confidence interval for the true proportion of adults in the town who have health insurance is approximately (0.7329, 0.8769).
**In percentage form:**
* (73.29%, 87.69%)
Question 1190594: A population consists of (3,8,10,15). Consider all possible sample size 2 that can be drawn with replacement.
-what is the standard deviation of the sampling distribution of means? =
-what is the population mean? =
-what is the population standard deviation? =
-what is the population variance? =
-what is the variance of the sampling distribution of means? =
-what is the mean of the sampling distribution of means? =
A population consists of (3,8,10,15). Consider all possible sample size
2 that can be drawn without replacement.
-what is the variance of the sampling distribution of means? =
-what is the standard deviation of the sampling distribution of means? =
-what is the mean of the sampling distribution of means? =
Answer by CPhill(1959) (Show Source):
You can put this solution on YOUR website! Here's how to calculate the requested values for both scenarios (with and without replacement):
**Scenario 1: With Replacement**
1. **Population Mean (μ):**
μ = (3 + 8 + 10 + 15) / 4 = 36 / 4 = 9
2. **Population Variance (σ²):**
σ² = [(3-9)² + (8-9)² + (10-9)² + (15-9)²] / 4
σ² = [36 + 1 + 1 + 36] / 4 = 74 / 4 = 18.5
3. **Population Standard Deviation (σ):**
σ = √σ² = √18.5 ≈ 4.3
4. **Variance of the Sampling Distribution of Means:**
When sampling with replacement, the variance of the sampling distribution of means (σₓ̄²) is given by:
σₓ̄² = σ² / n where n is the sample size.
σₓ̄² = 18.5 / 2 = 9.25
5. **Standard Deviation of the Sampling Distribution of Means (Standard Error):**
This is the square root of the variance of the sampling distribution:
σₓ̄ = √σₓ̄² = √9.25 ≈ 3.04
6. **Mean of the Sampling Distribution of Means (μₓ̄):**
When sampling with replacement, the mean of the sampling distribution of means is equal to the population mean:
μₓ̄ = μ = 9
**Scenario 2: Without Replacement**
1. **Population Mean (μ):** (Same as before)
μ = 9
2. **Population Variance (σ²):** (Same as before)
σ² = 18.5
3. **Population Standard Deviation (σ):** (Same as before)
σ ≈ 4.3
4. **Variance of the Sampling Distribution of Means:**
When sampling *without* replacement, the variance of the sampling distribution is adjusted by a finite population correction factor:
σₓ̄² = (σ² / n) * [(N - n) / (N - 1)]
Where N is the population size.
σₓ̄² = (18.5 / 2) * [(4 - 2) / (4 - 1)]
σₓ̄² = 9.25 * (2/3) = 6.17 (approximately)
5. **Standard Deviation of the Sampling Distribution of Means (Standard Error):**
σₓ̄ = √σₓ̄² = √6.17 ≈ 2.48
6. **Mean of the Sampling Distribution of Means (μₓ̄):**
Even when sampling without replacement, the mean of the sampling distribution of means is still equal to the population mean:
μₓ̄ = μ = 9
**Summary Table:**
| Statistic | With Replacement | Without Replacement |
|---|---|---|
| Population Mean (μ) | 9 | 9 |
| Population Variance (σ²) | 18.5 | 18.5 |
| Population Standard Deviation (σ) | 4.3 | 4.3 |
| Variance of Sampling Distribution (σₓ̄²) | 9.25 | 6.17 |
| Standard Error of the Mean (σₓ̄) | 3.04 | 2.48 |
| Mean of Sampling Distribution (μₓ̄) | 9 | 9 |
Question 1205257: 1. An investigator decided to construct a frequency distribution with five classes. The following
information was available. For fifty observations made on a characteristic under study, the
first two and the last two frequencies were 6,10,10 and 6 respectively. Given the last class
mark is 66 and upper class limit of the fifth class is 72.
a. Calculate mean, Median and mode.
Answer by CPhill(1959) (Show Source):
You can put this solution on YOUR website! ## Understanding the Problem
We have a frequency distribution with 5 classes and total observations = 50.
* First two class frequencies: 6, 10
* Last two class frequencies: 10, 6
* Last class mark: 66
* Upper limit of the last class: 72
## Constructing the Frequency Distribution Table
| Class Interval | Frequency (f) | Class Mark (x) | fx |
|---|---|---|---|
| | 6 | | |
| | 10 | | |
| | | | |
| | 10 | | |
| 66-72 | 6 | 69 | 414 |
## Finding Missing Values
1. **Class Width:**
* Class width = (Upper limit of last class - Lower limit of first class) / Number of classes
* Class width = (72 - Lower limit of first class) / 5
* We need to find the lower limit of the first class.
2. **Class Marks:**
* Class mark = (Upper limit + Lower limit) / 2
3. **Missing Frequencies:**
* Total frequency = 50
* Missing frequency = 50 - (6+10+10+6) = 18
## Completing the Table
Once we have the class width and missing frequency, we can complete the table. However, we still need more information to determine the exact class intervals and class marks.
**To proceed, we need either:**
1. **Lower limit of the first class:** This will allow us to calculate the class width and determine all class intervals and class marks.
2. **Class width:** This will allow us to determine the class intervals and class marks.
**Without this additional information, we cannot accurately calculate the mean, median, and mode.**
## Calculating Mean, Median, and Mode
Once we have the completed frequency distribution table, we can calculate these measures:
### Mean
* **Formula:** Mean = Σ(fx) / Σf
* Calculate Σfx by multiplying the frequency and class mark for each class, then summing these products.
* Divide Σfx by the total frequency (50).
### Median
* **Find the median class:** The median class is the class containing the 25th observation (halfway through the 50 observations).
* **Use the formula:** Median = L + [(N/2 - cf)/f] * h
* L = Lower limit of the median class
* N = Total frequency
* cf = Cumulative frequency of the class preceding the median class
* f = Frequency of the median class
* h = Class width
### Mode
* The mode is the class with the highest frequency.
Question 1204215: If limt(e^(ln(ax)) × tan(2a/x))= 8 ' find value of a ?
Found 2 solutions by ikleyn, MathLover1:
Answer by ikleyn(52779) (Show Source):
You can put this solution on YOUR website! .
In the post by @MathLover1, this woman made very rude mistakes, which show that
she not only does not know Calculus, but does not know the logarithmic function, as well.
Therefore, I will explain the solution from the very beginning.
If the problem asks about the limit at x---> -oo, then it is clear that the coefficient "a"
in this consideration must be negative - otherwise, logarithm ln(ax) is NOT DEFINED.
With negative "a", ln(ax) is defined at negative x, and we can write 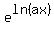 = ax.
Then
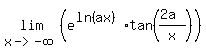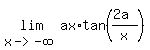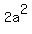 =  =  = 8,
which implies  = 4, and since "a" is negative, a = -2.
So, a = -2 is the only solution to this problem at x ---> -oo, which is exactly opposite to the conclusion by @MathLover1.
If the question is about finding "a" from this equation at x ---> oo, then the answer is a = 2.
Thus, the ANSWER is twofold: if x ---> -oo, then a = -2.
if x ---> oo, then a = 2.
Solved.
---------------
How this woman can call herself " MathLover1 ", making such errors, is a mystery to me.
Answer by MathLover1(20849)  (Show Source):
Question 1201121: The mean I.Q of a sample of 1600 children was 99. Is it likely that this was a random sample from a population with mean I.Q 100 and standard deviation 12? (Test at 5% level of significance)
Answer by math_tutor2020(3816) (Show Source):
You can put this solution on YOUR website!
Population info
mu = population mean = 100
sigma = population standard deviation = 12
Hypothesis:
Null: mu = 100
Alternative: mu =/= 100
The "not equals" in the alternative hypothesis indicates we'll be doing a two-tailed test.
Sample info
xbar = sample mean = 99
n = sample size = 1600
Compute the test statistic
z = (xbar - mu)/(sigma/sqrt(n))
z = (99 - 100)/(12/sqrt(1600))
z = -3.33 approximately
Use a Z table such as this one
https://www.ztable.net/
to find that
P(Z < -3.33) = 0.00043
This is the approximate area under the standard normal curve to the left of z = -3.33
We're doing a two-tailed test, so we double this area value.
2*0.00043 = 0.00086
This is the approximate p-value.
The p-value 0.00086 is smaller than alpha = 0.05, so we reject the null.
We conclude that the sample of 1600 children having a sample mean IQ of 99 very likely could not have been drawn from a population with mean IQ 100 and standard deviation 12.
Question 1200670: lim f(x)
x-1
Answer by ikleyn(52779) (Show Source):
Question 1200671: lim f(x)=2x^2-2x^2+3x-3
x-1
Answer by ikleyn(52779) (Show Source):
Question 1200672: lim f(x)=2x^2-2x^2+3x-3/x-1
x->1
Answer by ikleyn(52779) (Show Source):
You can put this solution on YOUR website! .
lim f(x)=2x^2-2x^2+3x-3/x-1
x->1
~~~~~~~~~~~~~~~~~~
I see some strange writing in your post f(x) = 2x^2 - 2x^2 and so on.
Normal people in healthy mind usually do not write in this way.
In addition, the parentheses absent in your post, making it unreadable or ambiguous.
Please be attentive when you post to this forum.
Question 1200673: lim g(x)=x^2-4/x+2
x->2
Answer by ikleyn(52779) (Show Source):
You can put this solution on YOUR website! .
The given function is continuous at the given point.
So, to find the limit, simply substitute the value x= 2 into the function and calculate.
The answer is 0 (zero).
Question 1200674: slope of the tangent line to the curve g(x)=x^2-4/x+2
Answer by ikleyn(52779) (Show Source):
You can put this solution on YOUR website! .
slope of the tangent line to the curve g(x)=x^2-4/x+2
~~~~~~~~~~~~~~~~~~
Your post is not complete - - - so I completed it and then answered :
slope of the tangent line to the curve g(x) = (x^2-4)/(x+2) at given point
is the derivative of the given function at the given point.
Question 1200399: 1. Each child born to a particular set of parents has a probability of 0.25 of having
blood type O. If these parents have 5 children. What is the probability that?
a. Exactly three of them have blood type O.
b. At most 2 have blood type O
c. At least 4 have no blood type O
d. The fifth child have blood type O
e. Compute the mean and variance of this probability distribution
f. Draw the probability distribution table
Answer by Solver92311(821)  (Show Source):
Question 1199283: The area of a rectangle is 46 square inches. If the length is 4 times the width, then find
the dimensions of the rectangle. Round off your answers to the nearest hundredth.
Answer by josgarithmetic(39617) (Show Source):
Question 1195851: Historically, 93% of the deliveries of an overnight mail service arrive before 10:30 the following morning. If a random sample of 500 deliveries is selected, what is the probability the sample will have more than 95% of the deliveries arriving before 10:30 the following morning?
Found 2 solutions by ikleyn, Boreal:
Answer by ikleyn(52779) (Show Source):
You can put this solution on YOUR website! .
Historically, 93% of the deliveries of an overnight mail service arrive before 10:30
the following morning. If a random sample of 500 deliveries is selected,
what is the probability the sample will have more than 95% of the deliveries arriving
before 10:30 the following morning?
~~~~~~~~~~~~~
In order for the mathematical and the probabilistic meaning of this problem
would become more clear, let me re-formulate it in this way.
There is a binomial distribution with the individual probability of success of 0.93.
There is a random sample of 500 trials.
What is the probability of more than 0.95*500 = 475 successful trials ?
In this formulation, the probability is a standard binomial distribution problem
P = P(n=500; k>=476; p=0.93).
To facilitate calculations, I use online calculator at this site https://stattrek.com/online-calculator/binomial.aspx
It provides nice instructions and a convenient input and output for all relevant options/cases.
The resulting number is P = 0.02796 (rounded). ANSWER
Solved.
Answer by Boreal(15235)  (Show Source):
You can put this solution on YOUR website! This is calculating a z-value which is here z=(phat-p)/sqrt (p*(1-p)/n)
=0.02/sqrt(0.93*0.07/500)
=0.02/0.0114
=1.75
Probability z > 1.75 is 0.0398
-
Can check with a normal approximation
mean is 0.93*500=465
variance is that *0.07=32.55
sd is sqrt of that=5.71
95% of 500 is 475
so z=(475.5-465)/5.71, using the continuity correction factor
=1.84 and the probability of z> 1.84 is 0.0329.
Question 1190595: SAMPLING DISTRIBUTION WITH AND WITHOUT REPLACEMENT
A population consists of (3,8,10,15). Consider all possible sample size 2 that can be drawn with replacement.
-what is the standard deviation of the sampling distribution of means? =
-what is the population mean? =
-what is the population standard deviation? =
-what is the population variance? =
-what is the variance of the sampling distribution of means? =
-what is the mean of the sampling distribution of means? =
A population consists of (3,8,10,15). Consider all possible sample size
2 that can be drawn without replacement.
-what is the variance of the sampling distribution of means? =
-what is the standard deviation of the sampling distribution of means? =
-what is the mean of the sampling distribution of means? =
Answer by MathLover1(20849) (Show Source):
Question 1186868: The mean height of an adult giraffe is 17 feet. Suppose that the distribution is normally distributed with standard deviation 0.9 feet. Let X be the height of a randomly selected adult giraffe. Round all answers to 4 decimal places where possible.
c. What is the Z-score for a giraffe that is 18.5 foot tall?
d. What is the probability that a randomly selected giraffe will be shorter than 17.5 feet tall?
e. What is the probability that a randomly selected giraffe will be between 16.7 and 17.2 feet tall?
f. The 70th percentile for the height of giraffes is
ft.
Answer by ikleyn(52779) (Show Source):
You can put this solution on YOUR website! .
The following instruction is how to answer questions (d) and (e).
=======================
Go to online (free of charge) normal distribution probability calculator
https://onlinestatbook.com/2/calculators/normal_dist.html
Input the given parameters of each part into the appropriate window of the calculator and get the answers
to your questions.
The calculator has perfect description and design, so EVERY person, even beginner, may work with it on his or her own,
even having minimum knowledge on the subject.
//////////////
Or, alternatively, you may use your GRAPHING CALCULATOR.
See THIS Internet source / site
https://mathbits.com/MathBits/TISection/Statistics2/normaldistribution.htm
Find there EVERYTHING you need to know in clear and compact form
to solve this problem (and thousand other) similar and different problems ON YOUR OWN.
Happy calculations ( ! )
Question 1184696: Let Y1, Y2, Y3, and Y4 be independent, identically distributed variables from a population with mean μ and variance σ(squared). let ȳ = 1/4(y1,y2,y3,y4) denote the average of these random variables. What are the expected value and variance in terms of μ and σ(squared)?
Answer by robertb(5830)  (Show Source):
Question 1178691: An advertising firm states that 27% of households will buy something on the Internet next year. How large a sample is needed to be 92% confident that this proportion is within 5% of true proportion.
Answer by robertb(5830) (Show Source):
Question 1179918: A recent survey indicated that the average amount spent for breakfast by business managers was $7.58 with a standard deviation of $0.42. It was felt that breakfasts on the West Coast were higher than $7.58. A sample of 81 business managers on the West Coast had an average breakfast cost of $7.65. Find the P-value for the test.
Answer by Theo(13342)  (Show Source):
You can put this solution on YOUR website! east coast population mean is 7.58 with standard deviation of .42
west coast sample mean is 7.65 with sample size = 81.
the standard error for the test is population standard deviation divided by sample size = .42 / sqrt(81) = .046666667 rounded to 9 decimal places.
the z-score is (sample mean minus population mean) / standard error.
this is equal to (7.65 - 7.58) / .046666667 = 1.5
area to the left of this z-score is .9331927713.
area to the right of this z-score is .0668072287.
the p-value for the test is the area to the right of this z-score.
since the test was whether the west coast average breakfast cost was higher than the east coast breakfast cost, then a one tailed confidence interval would be used to determine the significance of the test.
at 95% confidence interval, the critical p-value would be .05.
at 90% confidence interval, the critical p-value would be .10.
at .0668072287 p-value for the test, the results would be significant at 90 confidence interval but not significant at 95% confidence interval.
the most important calculation you would make would be to determine what the standard error for the test would be and whether or not a z-test or a t-test is indicated.
since you have the population standard deviation, and since the sample size is greater than 30, a z-test would be indicated.
the standard error is equal to the population standard deviation divided by the square root of the sample size.
that's why the standard error of the test was calculated to be .42/sqrt(81) = .046666667 rounded to the number of decimal places that the calculator was able to display.
rounding to 4 decimal places would have probably been good enough, but i just used what the calculator displayed.
if i had rounded to 4 decimal places, then the z-score would have been (7.65 - 7.58) / .0467 = 1.498929336 which i would have probably rounded to 1.499.
the p-value, in that case, would have been .0669 rounded to 4 decimal places.
either way, the result would have been the same.
the results were significant at 10% confidence level, but not significant at 5% significance level.
since the test was whether the sample mean was significantly greater than the population mean, the one tailed confidence interval was indicated.
here's a reference.
https://www.statisticshowto.com/one-sample-z-test/
Question 1178701: Annual precipitation in a certain city is normally distributed with a mean of 99 inches, and a standard deviation of 18 in. Find the probability that the mean annual precipitation during 35 randomly picked years will be less than 101.8 in.?
Answer by ikleyn(52779) (Show Source):
You can put this solution on YOUR website! .
For your education and for sake of your curiosity, look into the table
of Average Annual Precipitation by City in the United States
under this link
https://www.currentresults.com/Weather/US/average-annual-precipitation-by-city.php
Question 1178568: A random sample of 75 printers discovered that 25 of them were being used in small businesses . Find the 99% limit for the population proportion of printers that are used in small businesses.
Answer by JimmyJW(2)  (Show Source):
Question 1178567: A sample of size n=11 has a sample mean xbar=15.6 and sample standard deviation s=2.4. Construct a 95% confidence interval for the population mean μ.
Answer by ewatrrr(24785)  (Show Source):
Question 1178440: Of the members of a Boy Scout troop, 15% have received the first aid merit badge. If 40 boy scouts are selected at random, find the probability that four or more will have the first aid merit badge?
Answer by ikleyn(52779) (Show Source):
Question 1176929: 1,3,5 are the first three terms of a quadratic sequence the 7th term is 35 determine the 6th and 5th term of the sequence detrrmine the nth term
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
Incorrect statement of the problem....
The given first three terms form a linear sequence, not a quadratic sequence. Graphed as the three points (1,1), (2,3), and (3,5), the three points will lie on a straight line; no quadratic will ever contain three points in a straight line.
So if the sequence is quadratic, the given first three terms are not right.
And if the given first three terms are right and the sequence is linear, then the 7th term is not 35.
So nothing can be done with the given information....
Answer by ikleyn(52779) (Show Source):
You can put this solution on YOUR website! .
1,3,5 are the first three terms of a quadratic sequence the 7th term is 35
determine the 6th and 5th term of the sequence detrrmine the nth term
~~~~~~~~~~
Hello, the very first statement in your post is not correct --- it is WRONG (!)
The three numbers 1, 3, 5 do not form "a quadratic sequence".
They form a linear sequence, instead, which is the same as an arithmetic progression.
Use the terms properly, when you try to compose your own Math problem.
Question 1173381: Question :
The mean for the number of weeks 15 New York Times hard-cover fiction books spent on the bestseller list is 22 weeks. The standard deviation is 6.17 weeks. The mean for the number of weeks 15 New York Times hard-cover nonfiction books spent on the list is 28 weeks. The standard deviation is 13.2 weeks. At α=0.10, can we conclude that there is a difference in the mean times for the number of weeks the books were on the bestseller lists?
PLEASE REQUIRED DETAILED ANSWER:
Answer by Boreal(15235) (Show Source):
You can put this solution on YOUR website! Ho:means are equal for F and NF
Ha: means are not equal
alpha=0.10 p{reject Ho|Ho true}
test is a 2 sample t
critical value is t(0.95, df=28) is 1.701, reject if |t|>1.701
calculation is t=(difference between means)/sqrt[ (s1^2/n1)+(s2^2/n2)]
=-6/sqrt [(6.17^2/15)+(13.2^2/15)]; denominator=sqrt(14.15)
=-6/3.76
=-1.60
fail to reject Ho; insufficient evidence to say that there is a difference between the means.
p-value=0.13
Question 1173382: Question :
The mean life time of a sample of 90 light bulbs produced by a company is computed to be 1570 hours with a standard deviation of 120 hours. If µ is the mean of all bulbs produced by the company, test the hypothesis that µ is equal to 1600 hours against the alternative µ˂ 1600 hours.
Answer by Boreal(15235) (Show Source):
You can put this solution on YOUR website! This would be 1 way with a z-statistic which at the 0.05 level would have a critical value z < -1.645
z=(x bar-mean)/sigma/sqrt(90)
=-30*sqrt(90)/120
=-2.37
reject Ho; there is evidence that the true mean is < 1600 hrs. p-value=0.009.
Question 1163435: the area of a rectangle is 20 square inches. If the length is 4 inches less than 6 times the width, then find the dimensions of the rectangle. Round off your answer to the nearest hundredth.
Answer by greenestamps(13200) (Show Source):
Question 1161820: A trader sells at #30 each or #150 for six. How much do you save by buying three dozen eggs in sixes instead of separately?
Answer by ikleyn(52779) (Show Source):
You can put this solution on YOUR website! .
Buying three dozen eggs in sixes, you spend #150*2*3 = #600.
Buying three dozen eggs separately, you spend #30*3*12 = #1080.
You save #1080 - #600 = #480. ANSWER
Solved and answered.
Question 1159202:
Answer by ikleyn(52779) (Show Source):
Question 1158683: The maintenance department at the main campus of a large state university receives daily requests to replace fluorecent lightbulbs. The distribution of the number of daily requests is bell-shaped and has a mean of 49 and a standard deviation of 9. Using the 68-95-99.7 rule, what is the approximate percentage of lightbulb replacement requests numbering between 49 and 58?
Answer by Boreal(15235) (Show Source):
You can put this solution on YOUR website! 49 is the mean and 58 is 1 sd above the mean.
If 68% of all requests are between +/- 1 sd, then half or 34% are between 0 and +1 sd.
34% is the approximate percentage.
Question 1158684: A class is given an exam. The distribution of the scores is normal. The mean score is 80 and the standard deviation is 11. What is the probability that a student scored less than 78?
P(x < 78) =
Express the probability as a decimal rounded to 4 decimal places.
Answer by Boreal(15235) (Show Source):
You can put this solution on YOUR website! z=(x-mean)/sd
=(78-80)/11
probability z<-2/11 is 0.4279
We usually use z in the decimal form so here z=-0.182, but on a calculator one can use the fraction just as well.
2VARS 2 Normalcdf -6, -(2/11) . Note, I use -6 rather than 1E99 just for simplicity since 6 sd s from the mean will not change the result to four decimal places.
Question 1153704: Suppose certain coins have weights that are normally distributed with a mean of 5.661 g and a standard deviation of 0.057 g. A vending machine is configured to accept those coins with weights between 5.551 g and 5.771 g.
According to the certain limit theorem, the distribution of sample means x will have a mean given by u_x=u and a standard deviation given by o_x=o/sqrt n.
What is the mean of the distribution of sample means x? u_x=?
Answer by Boreal(15235) (Show Source):
Question 1153125: It takes 45 minutes to fill a circular pool with a depth of 18 inches. At this rate how long will it take to fill 35 inches.
Answer by Alan3354(69443)  (Show Source):
You can put this solution on YOUR website! It takes 45 minutes to fill a circular pool with a depth of 18 inches. At this rate how long will it take to fill 35 inches.
========================
circular pool with a depth of 18 inches.
---
If it's 18" deep, it will never be filled to 35 inches.
---
If it's >= 45" in depth:
45*(35/18) minutes
Question 1145363: Adult male height is normally distributed with a mean of 68.8 inches and a standard deviation of 2.31 inches. What adult male height separates the lower 64% from the upper 36%? Round your final answer to one decimal places.
Answer by VFBundy(438)  (Show Source):
You can put this solution on YOUR website! Go to a z-table and find the value closest to 0.64. The z-score that corresponds to this is 0.36. (NOTE: the z-score of 0.36 has nothing to do with the upper value of 36%. This is just a coincidence.)
 = 0.36
Cross-multiply:
x - 68.8 = 0.8316
x = 69.6316
So, the lower 64%/upper 36% point is 69.6 inches.
Question 1145360: A manufacturer knows that their items have a normally distributed lifespan, with a mean of 9.9 years, and standard deviation of 3.1 years.
The 4% of items with the shortest lifespan will last less than how many years?
Answer by VFBundy(438) (Show Source):
You can put this solution on YOUR website! Go to a z-table and find the value that corresponds with a score of 0.04. The closest z-score is -1.75.
Cross-multiply:
x - 9.9 = -5.425
x = 4.475
The 4% with the lowest lifespan will last less than 4.475 years.
Question 1145101: The human adult male height population has a mean M= 70 and a standard deviation of of 4 (measures given in inches), for human adult females M= 65 and standard deviation of 3.5, also in inches.
Answer by richwmiller(17219)  (Show Source):
Question 1145103: The human adult male height population has a mean M= 70 and a standard deviation of of 4 (measures given in inches), for human adult females M= 65 and standard deviation of 3.5, also in inches.
Answer by richwmiller(17219) (Show Source):
Question 1145104: The human adult male height population has a mean M= 70 and a standard deviation of 4 (measures given in inches), for human adult females M= 65 and standard deviation of 3.5, also in inches.
Answer by richwmiller(17219) (Show Source):
Question 1143157: A manufacturer knows that their items have a normally distributed lifespan, with a mean of 8.5 years, and standard deviation of 1.2 years.
If you randomly purchase 16 items, what is the probability that their mean life will be longer than 8 years?
Answer by rothauserc(4718)  (Show Source):
You can put this solution on YOUR website! The probability(P) that their mean life will be longer than 8 years = 1 - P(X < 8)
:
Since the population standard deviation is known, we can use the normal distribution for the sample with the standard error
:
standard error(SE) = population standard deviation/square root of sample size
:
SE = 1.2/square root(16) = 1.2/4 = 0.3
:
z-score(8) = (8 - 8.5)/0.3 = −1.6667 is approximately -1.67
:
P associated with z-score of −1.67 is 0.0475 (use z-score tables)
:
************************************************
P(X > 8) = 1 - P(X < 8) = 1 - 0.0475 = 0.9525
***********************************************
:
Question 1139135: Preston received a paycheck for $900.00 and he wants to invest it in a savings account. A savings account at bank A earns 4% interest compounded monthly and a savings account at bank B earns 5% simple interest. If Preston plans to deposit the $900.00 and leave it in the account for 3 years, at which bank would he earn more interest?
Answer by josmiceli(19441)  (Show Source):
Question 1131223: The average annual cost of the first year of owning and caring for a large dog is $1843 (US News and World Report, September 9, 2013). The Irish Red and White Setter Association of America has requested a study to estimate the annual first-year cost for owners of this breed. A sample of 50 will be used. Based on past studies, the population standard deviation is assumed known with σ = $255.
a) What is the margin of error for a 95% confidence interval of the mean cost of the first year of owning and caring for this breed?
b) The DATAfile Setters contains data collected from fifty owners of Irish Setters on the cost of the first year of owning and caring for their dogs. Use these data sets to compute the sample mean. Using this sample, what is the 95% confidence interval for the mean cost of the first year of owning and caring for an Irish Red and White Setter?
Answer by Boreal(15235) (Show Source):
You can put this solution on YOUR website! the margin of error is z0.975)*sigma/sqrt(n)=1.96*255/sqrt(50)=$70.68
The interval cannot be constructed without the data, but it would be the mean +/- error shown above.
Question 1128748: A raffle has a grand prize of a Caribbean cruise valued at $14,000 with for each ticketa second prize of a Las Vegas getaway valued at $800. If each ticket costs $5 and 8800 tickets are sold, what are the expected winnings far a ticket buyer? Round to the nearest penny.
Answer by greenestamps(13200) (Show Source):
You can put this solution on YOUR website!
(1/8880) * $14,000 for the grand prize
(1/8880) * $800 for the second prize
Total expected value:
The expected winnings (payout) is 5/3 of a dollar for each ticket. To the nearest penny, that is $1.67.
If you include the $5 cost of the ticket, the expected "winnings" is $1.67-$5 = -$3.33.
|
|
