Question 1201530: I have to simplify the following - all base 10 logarithms:
log(a)-1/2log(4a)
I get this far:
log(a) - log(4a)^1/2
log[a/(4a)^1/2]
but then I get stuck!
Found 6 solutions by Edwin McCravy, Theo, mccravyedwin, ikleyn, MathTherapy, n3:
Answer by Edwin McCravy(20064)   (Show Source):
You can put this solution on YOUR website!
I deleted the solution I had posted here because I mistook your given
instructions. See my solution at the bottom which is a continuation
of what you did.
Edwin
Answer by Theo(13342)  (Show Source):
You can put this solution on YOUR website! equation is:
log(a) - 1/2 * log(4a) which is equal to:
log(a) - log((4a)^(1/2)) which is equal to:
log(a) - log(2 * a ^ (1/2)) which is equal to:
log(a / (2 * a ^ (1/2))) which is equal to:
log(1/2 * a / a ^ (1/2)) which is equal to:
log(1/2 * a ^ (1/2))
that, i believe, is as simple as it gets.
to see if this is true, give a randomly selected value and see if the original equation gives the same result at the simplified equation.
i chose a = 90.
original equation gives result of .6760912591
simplified equation gives the same result.
this confirms the simplification is correct.
i saw a mistake that you made in the simplification process.
1/2 * log(4a) is equal to log((4a) ^ (1/2)), not log(4 * a^(1/2)).
oops.
you didn't make a mistake.
i read it wrong.
sorry about that.
everything else i said applies.
let me know if you have any questions.
theo
Answer by mccravyedwin(409)  (Show Source):
Answer by ikleyn(52879)  (Show Source):
You can put this solution on YOUR website! I have to simplify the following - all base 10 logarithms:
log(a)-1/2log(4a)
I get this far:
log(a) - log(4a)^1/2
log[a/(4a)^1/2]
but then I get stuck!
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Using the standard rules of logarithms, solve it this way
log(a) - (1/2)*log(4a) = log(a) - (1/2) * [log(4) + log(a)] = log(a) - (1/2)*log(4) - (1/2)*log(a) (*)
Combine the 1st and the 3rd terms in (*) log(a) - (1/2)*log(a) = (1/2)*log(a).
Transform the 2nd term in (*) (1/2)*log(4) = (1/2) * (2*log(2)) = log(2).
So, you can continue line (*) in this way
log(a) - (1/2)*log(4a) = (1/2)*log(a) - log(2). (1)
The rest depends for whom you do this assignment.
If it is a Math assignment, then you transform right side of (1) into
log(a) - (1/2)*log(4a) =  .
It gives you the answer in simplest mathematical form.
If you simplify for "Computer Science", they prefer another form as a "simplest"
log(a) - (1/2)*log(4a) = (1/2)*log(a) - log(2), (2)
same as (1).
Why ? - - - because, firstly, then we do not need calculate  ,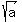
and, secondly, log(2) can be considered as a constant.
So, if there is the need to compute log(a) - (1/2)*log(4a) many times for different values of 'a'
(as it often happens in computing), then form (2) is preferable.
For computing, they do not use the term "simplest form" of an expression.
Instead, they think about the form, which is most  for calculations,
i.e. requires minimum of arithmetic operations.
Solved, with explanations.
Answer by MathTherapy(10556)  (Show Source):
Answer by n3(2)  (Show Source):
|
|
|
