Algebra.Com's Answer #832994 by Shin123(626)  
You can put this solution on YOUR website!
Let  be the amount (in kilograms) of Candy A that is produced, and let be the amount (in kilograms) of Candy A that is produced, and let  be the amount of Candy B that is produced. The profit that the manufacturer makes is be the amount of Candy B that is produced. The profit that the manufacturer makes is 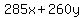 . However, the constraints are that . However, the constraints are that  , ,  , and , and  . .
\n" );
document.write( "We can see that it is optimal to have  , since moving it off of that line would only decrease the profit. Multiplying both sides of that by , since moving it off of that line would only decrease the profit. Multiplying both sides of that by  , we get , we get  . Adding . Adding 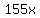 to both sides, we get to both sides, we get  . We can see that we got out profit into a form that doesn't involve . We can see that we got out profit into a form that doesn't involve  at all, so we should just maximize at all, so we should just maximize  . The highest value of . The highest value of  that satisfies all of the constriants is that satisfies all of the constriants is  . Therefore, the candy manufacturer should produce . Therefore, the candy manufacturer should produce  kilograms of Candy A, and kilograms of Candy A, and  kilograms of Candy B. \n" );
document.write( " kilograms of Candy B. \n" );
document.write( " |



