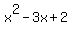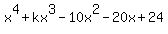document.write( "Question 1189239: Given that $\"+x%5E2-3x%2B2+\"$ is a factor of $\"+x%5E4+%2B+kx%5E3+-+10x%5E2+-+20x%2B24+\"$ evaluate the sum of the four roots of the equation $\"+x%5E4+%2B+kx%5E3+-+10x%5E2+-+20x%2B24+=+0+\"$ \n" ); document.write( "

Algebra.Com's Answer #820627 by MathTherapy(10552) $\"\"$ $\"About$

You can put this solution on YOUR website!
Given that $\"+x%5E2-3x%2B2+\"$ is a factor of $\"+x%5E4+%2B+kx%5E3+-+10x%5E2+-+20x%2B24+\"$ evaluate the sum of the four roots of the equation $\"+x%5E4+%2B+kx%5E3+-+10x%5E2+-+20x%2B24+=+0+\"$
\n" ); document.write( "

When factored,  = (x - 1)(x - 2).
\n" );
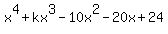document.write( "As  is a factor of , x - 1 and x - 2 are also factors of 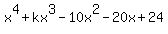, which 
\n" );
document.write( "means that x - 1 = 0, or x = 1, and x - 2 = 0, or x = 2. So, 2 of the roots of 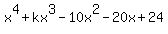 are 1 and 2.
\n" );
document.write( "Using either root, and the RATIONAL ROOT THEOREM, we find that k = 5.\r
\n" );
document.write( "\n" );
document.write( "The equation 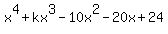 now becomes: 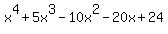, and when POLYNOMIAL LONG-DIVISION and its
\n" );
document.write( "factor,  are used, the other factor of the polynomial,  is derived. 
\n" );
document.write( "And, when  is factored, its roots, from its factors x + 6 and x + 2, are - 6 and - 2.
\n" );
document.write( "We now have roots: 1, 2, - 6, and - 2. 
\n" );
document.write( "Therefore, the sum of the roots of 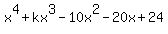 or 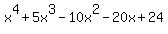 = 1 + 2 + (- 6) + (- 2) = - 5. \n" );
document.write( "

\n" );