Algebra.Com's Answer #780603 by Shin123(626)  
You can put this solution on YOUR website!
If  and and 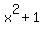 are inverses, than f(g(x))=x and g(f(x))=x are inverses, than f(g(x))=x and g(f(x))=x  . .  , which does not equal x. It equals , which does not equal x. It equals 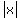 , not x. Therefore, f(x) and g(x) are not inverses. However, if you restrict the domain of g to , not x. Therefore, f(x) and g(x) are not inverses. However, if you restrict the domain of g to  , then f and g are inverses. \n" );
document.write( " , then f and g are inverses. \n" );
document.write( " |



