document.write( "Question 1156238: Identify the degree of the polynomial. Find all zeros (real and imaginary) and indicate their multiplicity if greater than 1.
\n" ); document.write( " $\"P%28x%29=%28x++-++8%29%5E3%28x%5E2+%2B49%29%284x%5E2++-++12x++-++1%29\"$ \n" ); document.write( "

Algebra.Com's Answer #778941 by Edwin McCravy(20060) $\"\"$ $\"About$

You can put this solution on YOUR website!

\r\n" );
document.write( "There is no need to multiply that out, collect terms and write in descending\r\n" );
document.write( "order.  But I went ahead and did it anyway, and got:\r\n" );
document.write( "\r\n" );
document.write( "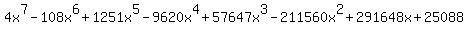\r\n" );
document.write( "\r\n" );
document.write( "So we see that the degree is 7, the largest exponent of x.\r\n" );
document.write( "\r\n" );
document.write( "However, we could have told that by observing that the factor (x-8)³ would\r\n" );
document.write( "contribute a term in x³, the factor (x²+49) would contribute a term in x²\r\n" );
document.write( "and the factor (4x²-12x-1) would contribute a term in x², so we add the\r\n" );
document.write( "powers 3+2+2=7 and know that the degree is 7 without multiplying it out.\r\n" );
document.write( "\r\n" );
document.write( "To find all the zeros, we set the right side of P(x) equal to zero and use the\r\n" );
document.write( "zero-factor property:\r\n" );
document.write( "\r\n" );
document.write( " \r\n" );
document.write( "\r\n" );
document.write( "\r\n" );
document.write( "\r\n" );
document.write( "(x-8)³ = 0; x²+49 = 0;   4x²-12x-1 = 0\r\n" );
document.write( "   x-8 = 0;    x² = 49;\r\n" );
document.write( "     x = 8;     x = ±7i;\r\n" );
document.write( "\r\n" );
document.write( "The 8 has multiplicity 3.\r\n" );
document.write( "That's because if we wrote \r\n" );
document.write( "(x-8)³ \r\n" );
document.write( "as\r\n" );
document.write( "(x-8)(x-8)(x-8) = 0\r\n" );
document.write( "we would have\r\n" );
document.write( "x-8=0; x-8=0; x-8=0\r\n" );
document.write( "  x=8;   x=8;   x=8\r\n" );
document.write( "\r\n" );
document.write( "and 8 would be a zero three times.\r\n" );
document.write( "\r\n" );
document.write( "The last one won't factor, so we use the quadratic formula\r\n" );
document.write( "\r\n" );
document.write( "\r\n" );
document.write( "\r\n" );
document.write( "\r\n" );
document.write( "\r\n" );
document.write( "\r\n" );
document.write( "\r\n" );
document.write( "\r\n" );
document.write( "\r\n" );
document.write( "\r\n" );
document.write( "So the zeros are\r\n" );
document.write( "\r\n" );
document.write( "8 with multiplicity 3\r\n" );
document.write( "7i with multiplicity 1\r\n" );
document.write( "-7i with multiplicity 1\r\n" );
document.write( "\r\n" );
document.write( "with multiplicity 1\r\n" );
document.write( "and\r\n" );
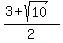document.write( "\r\n" );
document.write( "with multiplicity 1\r\n" );
document.write( "\r\n" );
document.write( "Edwin

\n" ); document.write( "

\n" );