Algebra.Com's Answer #623326 by cparks1000000(5)  
You can put this solution on YOUR website!
The previous solution is incorrect. Let me correct it:\r
\n" );
document.write( "\n" );
document.write( "Assume  is rational. Then there exists integers is rational. Then there exists integers  and and  such that such that  . Then by Zorn's lemma, there exists a greatest common divisor of . Then by Zorn's lemma, there exists a greatest common divisor of  and and  , say it is , say it is  . Set . Set  such that such that  and and  such that such that  . Then by definition of the rationals, . Then by definition of the rationals,  . But then . But then  divides divides  . Then by definition of the rationals, . Then by definition of the rationals,  . This is true since if we assume that . This is true since if we assume that  divides divides  ; then we can use the unique factorization theorem to conclude that ; then we can use the unique factorization theorem to conclude that  where all of the where all of the  are prime and none of them are 7. Thus are prime and none of them are 7. Thus  divides divides  which is a contradiction since it obviously has no factors which are which is a contradiction since it obviously has no factors which are  since since  is prime. Thus we have that is prime. Thus we have that  divides divides 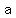 . Since . Since  divides divides  , there exists , there exists  such that such that  , thus , thus  . Thus by similar logic to the above, we have . Thus by similar logic to the above, we have  divides divides  . Since . Since  divides divides  we can use the prime factorization theorem to once again conclude that we can use the prime factorization theorem to once again conclude that  divides divides  . But then . But then  and and  must have a common factor. This is a contraction. Thus must have a common factor. This is a contraction. Thus 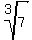 is irrational. \n" );
document.write( " is irrational. \n" );
document.write( " |



