In order to factor  , first we need to ask ourselves: What two numbers multiply to -1 and add to 0? Lets find out by listing all of the possible factors of -1
\n" );
document.write( "
\n" );
document.write( "
\n" );
document.write( " Factors:
\n" );
document.write( "
\n" );
document.write( " 1,
\n" );
document.write( "
\n" );
document.write( " -1,List the negative factors as well. This will allow us to find all possible combinations
\n" );
document.write( "
\n" );
document.write( " These factors pair up to multiply to -1.
\n" );
document.write( "
\n" );
document.write( " (-1)*(1)=-1
\n" );
document.write( "
\n" );
document.write( " Now which of these pairs add to 0? Lets make a table of all of the pairs of factors we multiplied and see which two numbers add to 0
\n" );
document.write( "
\n" );
document.write( " | First Number | | | Second Number | | | Sum | | 1 | | | -1 | || | 1+(-1)=0 | | -1 | | | 1 | || | (-1)+1=0 | We can see from the table that -1 and 1 add to 0.So the two numbers that multiply to -1 and add to 0 are: -1 and 1\r\n" );
document.write( " \r\n" );
document.write( " Now we substitute these numbers into a and b of the general equation of a product of linear factors which is:\r\n" );
document.write( " \r\n" );
document.write( " 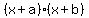 substitute a=-1 and b=1\r\n" );
document.write( " \r\n" );
document.write( " So the equation becomes:\r\n" );
document.write( " \r\n" );
document.write( " (x-1)(x+1)\r\n" );
document.write( " \r\n" );
document.write( " Notice that if we foil (x-1)(x+1) we get the quadratic again\n" );
document.write( "
\n" );
document.write( "
\n" );
document.write( "
\n" );
document.write( "\n" );
document.write( "Now factor  \r
\n" );
document.write( "\n" );
document.write( "\n" );
document.write( "\n" );
document.write( " | Solved by pluggable solver: Factoring Quadratics with a leading coefficient of 1 (a=1) | \n" );
document.write( "In order to factor  , first we need to ask ourselves: What two numbers multiply to -3 and add to 2? Lets find out by listing all of the possible factors of -3
\n" );
document.write( "
\n" );
document.write( "
\n" );
document.write( " Factors:
\n" );
document.write( "
\n" );
document.write( " 1,3,
\n" );
document.write( "
\n" );
document.write( " -1,-3,List the negative factors as well. This will allow us to find all possible combinations
\n" );
document.write( "
\n" );
document.write( " These factors pair up to multiply to -3.
\n" );
document.write( "
\n" );
document.write( " (-1)*(3)=-3
\n" );
document.write( "
\n" );
document.write( " Now which of these pairs add to 2? Lets make a table of all of the pairs of factors we multiplied and see which two numbers add to 2
\n" );
document.write( "
\n" );
document.write( " | First Number | | | Second Number | | | Sum | | 1 | | | -3 | || | 1+(-3)=-2 | | -1 | | | 3 | || | (-1)+3=2 | We can see from the table that -1 and 3 add to 2.So the two numbers that multiply to -3 and add to 2 are: -1 and 3\r\n" );
document.write( " \r\n" );
document.write( " Now we substitute these numbers into a and b of the general equation of a product of linear factors which is:\r\n" );
document.write( " \r\n" );
document.write( " 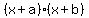substitute a=-1 and b=3\r\n" );
document.write( " \r\n" );
document.write( " So the equation becomes:\r\n" );
document.write( " \r\n" );
document.write( " (x-1)(x+3)\r\n" );
document.write( " \r\n" );
document.write( " Notice that if we foil (x-1)(x+3) we get the quadratic again\n" );
document.write( "
\n" );
document.write( "
\n" );
document.write( "
\n" );
document.write( "\n" );
document.write( "So after all of that we get \r
\n" );
document.write( "\n" );
document.write( " \r
\n" );
document.write( "
\n" );
document.write( "\n" );
document.write( " Notice these terms cancel\r
\n" );
document.write( "\n" );
document.write( "So we're left with\r
\n" );
document.write( "\n" );
document.write( " \r
\n" );
document.write( "
\n" );
document.write( "\n" );
document.write( " Multiply\r
\n" );
document.write( "
\n" );
document.write( "\n" );
document.write( " \r
\n" );
document.write( "
\n" );
document.write( "\n" );
document.write( " Divide \r
\n" );
document.write( "\n" );
document.write( "So the expression  reduces to \r
\n" );
document.write( "\n" );
document.write( " \n" );
document.write( "
\n" );
|
|
![\"\"](\"/images/stars/stars-13.gif\")
