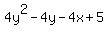
document.write( "Question 830525: $\"4y%5E2-4y-4x%2B5=0\"$
\n" ); document.write( "How do I write that in standard form? I've tried many ways. \n" ); document.write( "

Algebra.Com's Answer #500724 by Edwin McCravy(20060) $\"\"$ $\"About$

You can put this solution on YOUR website!

\r\n" );
document.write( "\r\n" );
document.write( "\r\n" );
document.write( "You want it to look like this\r\n" );
document.write( "\r\n" );
document.write( "\r\n" );
document.write( "\r\n" );
document.write( "which is a parabola with a horizontal axis of symmetry that\r\n" );
document.write( "either opens left or right. We can't tell which yet.  It\r\n" );
document.write( "has a vertex of (h,k)\r\n" );
document.write( "\r\n" );
document.write( "\r\n" );
document.write( "\r\n" );
document.write( "Get the y-terms on the left and everything else on the right\r\n" );
document.write( "\r\n" );
document.write( "\r\n" );
document.write( "\r\n" );
document.write( "Divide every term by 4\r\n" );
document.write( "\r\n" );
document.write( "\r\n" );
document.write( "\r\n" );
document.write( "Complete the square on the left side:\r\n" );
document.write( "\r\n" );
document.write( "1. To the side, multiply the coefficient of y, which is -1, by ,\r\n" );
document.write( "   getting \r\n" );
document.write( "2. Square the result of 1.  \r\n" );
document.write( "3. Add the result of 2 to both sides of the equation:\r\n" );
document.write( "\r\n" );
document.write( "\r\n" );
document.write( "\r\n" );
document.write( "Factor the left side:  \r\n" );
document.write( "Combine the numbers on the right \r\n" );
document.write( "\r\n" );
document.write( "\r\n" );
document.write( "\r\n" );
document.write( "To show the 4p in the standard equation, perhaps your teacher\r\n" );
document.write( "wants you to put a 1 factor on the right side:\r\n" );
document.write( "\r\n" );
document.write( "\r\n" );
document.write( "\r\n" );
document.write( "and now it corresponds exactly to\r\n" );
document.write( "\r\n" );
document.write( "\r\n" );
document.write( "\r\n" );
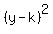
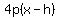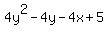
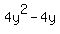
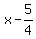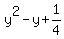
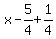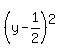
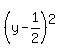
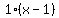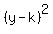
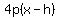document.write( "The vertex is (h,k) = (1,)\r\n" );
document.write( "\r\n" );
document.write( "4p=1, so p=, since p is positive it opens right.\r\n" );
document.write( "\r\n" );
document.write( "Its focus is the point  unit right of its vertex,\r\n" );
document.write( "at (1,), and the latus rectum is 4p=1 unit long\r\n" );
document.write( "through the focus.  The directrix line is the vertical \r\n" );
document.write( "line  unit left of the vertex.  It has the \r\n" );
document.write( "equation . to 4p = 1 unit. So we draw the \r\n" );
document.write( "vertex, focus, directrix and latus rectum and we have this:\r\n" );
document.write( "\r\n" );
document.write( "\r\n" );
document.write( "\r\n" );
document.write( "Then we sketch in the parabola:\r\n" );
document.write( "\r\n" );
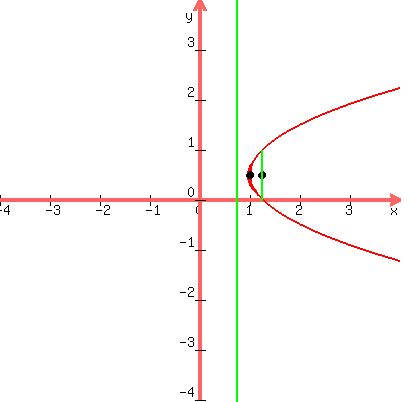document.write( "\r\n" );
document.write( "\r\n" );
document.write( "Yes, I know you didn't need to graph it but you'll have to later.\r\n" );
document.write( "\r\n" );
document.write( "Edwin

\n" ); document.write( "

\n" );