document.write( "Question 630556: Solve the equation for exact solutions over the interval [0,2 $\"pi\"$ ).\r
\n" ); document.write( "\n" ); document.write( " tan(x) + sec(x) = 1 \n" ); document.write( "

Algebra.Com's Answer #396996 by Edwin McCravy(20060) $\"\"$ $\"About$

You can put this solution on YOUR website!

\r\n" );
document.write( "tan(x) + sec(x) = 1\r\n" );
document.write( "\r\n" );
document.write( " +  = 1\r\n" );
document.write( "\r\n" );
document.write( "Multiply through by LCD of cos(x)\r\n" );
document.write( "\r\n" );
document.write( "sin(x) + 1 = cos(x)\r\n" );
document.write( "\r\n" );
document.write( "sin(x) - cos(x) = -1\r\n" );
document.write( "\r\n" );
document.write( "Since sin() = cos() = \r\n" );
document.write( "\r\n" );
document.write( "We can use that fact to make the left side into the the form of\r\n" );
document.write( "the right side of the identity \r\n" );
document.write( "\r\n" );
document.write( "We multiply through by \r\n" );
document.write( "\r\n" );
document.write( "sin(x) - cos(x) = -1\r\n" );
document.write( "\r\n" );
document.write( "Write the first  in the first term as cos() and\r\n" );
document.write( "the  in the second term as sin():\r\n" );
document.write( "\r\n" );
document.write( "sin(x)cos() - cos(x)sin() = \r\n" );
document.write( "\r\n" );
document.write( "Using the identity , we can rewrite the left side as\r\n" );
document.write( "\r\n" );
document.write( "sin(x-) = \r\n" );
document.write( "\r\n" );
document.write( "Therefore x- must be a 3rd or 4th quadrant angle to have\r\n" );
document.write( "a negative value for its sine.   \r\n" );
document.write( "\r\n" );
document.write( "Since 0 ≦ x < 2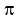 we subtract  from all three sides:\r\n" );
document.write( "\r\n" );
document.write( "    0- ≦ x-2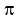 < 2pi- \r\n" );
document.write( "      \r\n" );
document.write( "     ≦ x-2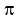 <  \r\n" );
document.write( "\r\n" );
document.write( "The only angle in that interval which has a sine of  \r\n" );
document.write( "is 4th quadrant angle  \r\n" );
document.write( "       \r\n" );
document.write( "\r\n" );
document.write( "x- =         \r\n" );
document.write( "\r\n" );
document.write( "Solving for x:\r\n" );
document.write( "\r\n" );
document.write( "   x =  + \r\n" );
document.write( "\r\n" );
document.write( "   x = 0\r\n" );
document.write( "\r\n" );
document.write( "It checks in the original (sometimes there are extraneous answers)\r\n" );
document.write( "\r\n" );
document.write( "\r\n" );
document.write( "tan(x) + sec(x) = 1\r\n" );
document.write( "tan(0) + sec(0) = 1\r\n" );
document.write( "          0 + 1 = 1   \r\n" );
document.write( "\r\n" );
document.write( "x = 0 is the only solution!\r\n" );
document.write( "\r\n" );
document.write( "Edwin

\n" ); document.write( "

\n" );