document.write( "Question 555695: sin[cos^-1( $\"12%2F13\"$ )]. Give as a fraction.
\n" ); document.write( " \n" ); document.write( "

Algebra.Com's Answer #361911 by Edwin McCravy(20060) $\"\"$ $\"About$

You can put this solution on YOUR website!
sin[cos^-1( $\"12%2F13\"$ )]. Give as a fraction.
\n" ); document.write( "

\r\n" );
document.write( "First we look at the inside only:\r\n" );
document.write( "\r\n" );
document.write( "cos^-1()  \r\n" );
document.write( "\r\n" );
document.write( "That is the answer to this question:\r\n" );
document.write( "\r\n" );
document.write( "What is the smallest angle in absolute value which has \r\n" );
document.write( "for its cosine?\r\n" );
document.write( "\r\n" );
document.write( "The answer to that question is an angle in the first quadrant.\r\n" );
document.write( "We don't know right off without a calculator what that angle is.\r\n" );
document.write( "However we can DRAW IT in standard position, because we know that\r\n" );
document.write( "the cosine is  or , so we\r\n" );
document.write( "draw this right triangle in the first quadrant, with the adjacent \r\n" );
document.write( "side equal to the numerator of the fraction, x=12, and the hypotenuse\r\n" );
document.write( "equal to the denominator of the fraction, r=13.  So we draw this:\r\n" );
document.write( "\r\n" );
document.write( "\r\n" );
document.write( "\r\n" );
document.write( "The angle indicated by the red arc is the angle represented by\r\n" );
document.write( "\r\n" );
document.write( "cos^-1()\r\n" );
document.write( "\r\n" );
document.write( "[I realize that it takes a while to get used to something that\r\n" );
document.write( "starts with \"COSINE\" to represent an ANGLE, but that's what\r\n" );
document.write( "the little \"-1\" does. (It's not really a -1, nor is it an exponent,\r\n" );
document.write( "but unfortunately the mathematicians of old used that notation and \r\n" );
document.write( "it stuck, so we are stuck with it, but it is NOT -1 and it is not\r\n" );
document.write( "an exponent. cos^-1 represents an ANGLE which has what follows it as\r\n" );
document.write( "its cosine.)]\r\n" );
document.write( "\r\n" );
document.write( "Now let's go back to the original problem:\r\n" );
document.write( "\r\n" );
document.write( "sin[cos^-1()]\r\n" );
document.write( "\r\n" );
document.write( "We want the SINE of that angle indicated by the red arc and\r\n" );
document.write( "represented by cos^-1().\r\n" );
document.write( "\r\n" );
document.write( "The sine is 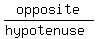, or , so we will \r\n" );
document.write( "have to find the opposite side of that angle, which is the y value.\r\n" );
document.write( "\r\n" );
document.write( "So we call on old man Pythagorus:\r\n" );
document.write( "\r\n" );
document.write( " r² = x² + y²\r\n" );
document.write( "13² = 12² + y²\r\n" );
document.write( "169 = 144 + y²\r\n" );
document.write( " 25 = y²\r\n" );
document.write( "  5 = y\r\n" );
document.write( "\r\n" );
document.write( "So we get y = 5, so we put that over on the right of the drawing:\r\n" );
document.write( "\r\n" );
document.write( "\r\n" );
document.write( " \r\n" );
document.write( "Now we can find that sine easily as 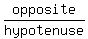 or \r\n" );
document.write( "or  \r\n" );
document.write( "\r\n" );
document.write( "So sin[cos^-1()] = \r\n" );
document.write( "\r\n" );
document.write( "Edwin

\n" ); document.write( "

\n" );