Algebra.Com's Answer #115597 by phd(3)  
You can put this solution on YOUR website!
Consider Jack's rate as  lawn per hour and Mary's rate as lawn per hour and Mary's rate as  lawn per hour. Together they have a rate of lawn per hour. Together they have a rate of  . Thus in one hour they can mow . Thus in one hour they can mow 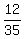 of the lawn. Now the rate times the time it takes them will give you one whole lawn. So, since they are mowing just one lawn take the reciprocal of of the lawn. Now the rate times the time it takes them will give you one whole lawn. So, since they are mowing just one lawn take the reciprocal of 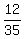 which is which is 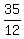 and this is how many hours it takes them to mow a lawn together. Now this might be easier to see in minutes. If we divided 35 by 12 we get 2 with 11 left over. So and this is how many hours it takes them to mow a lawn together. Now this might be easier to see in minutes. If we divided 35 by 12 we get 2 with 11 left over. So  hours. Thinking of a clock which has 12 numbers. The 11 on a clock represents 55 minutes. Another way of looking at that is that hours. Thinking of a clock which has 12 numbers. The 11 on a clock represents 55 minutes. Another way of looking at that is that  and there are 60 minutes in one hour. Therefore the answer is 2 hours and 55 minutes which is less time than it take either of them alone. \n" );
document.write( " and there are 60 minutes in one hour. Therefore the answer is 2 hours and 55 minutes which is less time than it take either of them alone. \n" );
document.write( " |



