what is the geometric series 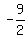 +
+ +
+ +
+ -...+
-...+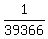 in summation notation?
in summation notation?
\n" );
document.write( "\r\n" );
document.write( " \r\n" );
document.write( "\r\n" );
document.write( "\r\n" );
document.write( "We divide the 2nd term by the 1st term to find the common ratio
\r\n" );
document.write( "\r\n" );
document.write( "\r\n" );
document.write( "We divide the 2nd term by the 1st term to find the common ratio  \r\n" );
document.write( "\r\n" );
document.write( "
\r\n" );
document.write( "\r\n" );
document.write( " \r\n" );
document.write( "\r\n" );
document.write( "To check we divide the 3rd term by the 2nd term to see if we get the \r\n" );
document.write( "same common ratio
\r\n" );
document.write( "\r\n" );
document.write( "To check we divide the 3rd term by the 2nd term to see if we get the \r\n" );
document.write( "same common ratio  :\r\n" );
document.write( "\r\n" );
document.write( "
:\r\n" );
document.write( "\r\n" );
document.write( " \r\n" );
document.write( "\r\n" );
document.write( "To double check we divide the 4th term by the 3rd term to see if we get the \r\n" );
document.write( "same common ratio
\r\n" );
document.write( "\r\n" );
document.write( "To double check we divide the 4th term by the 3rd term to see if we get the \r\n" );
document.write( "same common ratio  :\r\n" );
document.write( "\r\n" );
document.write( "
:\r\n" );
document.write( "\r\n" );
document.write( " \r\n" );
document.write( "\r\n" );
document.write( "Now that we are triple-sure that the common ratio
\r\n" );
document.write( "\r\n" );
document.write( "Now that we are triple-sure that the common ratio  ,\r\n" );
document.write( "\r\n" );
document.write( "we will use the formula for the nth term:\r\n" );
document.write( "\r\n" );
document.write( "
,\r\n" );
document.write( "\r\n" );
document.write( "we will use the formula for the nth term:\r\n" );
document.write( "\r\n" );
document.write( " \r\n" );
document.write( "\r\n" );
document.write( "to find out how many terms it has:\r\n" );
document.write( "\r\n" );
document.write( "
\r\n" );
document.write( "\r\n" );
document.write( "to find out how many terms it has:\r\n" );
document.write( "\r\n" );
document.write( " is the last, or nth, term:\r\n" );
document.write( "
is the last, or nth, term:\r\n" );
document.write( " is the first term\r\n" );
document.write( "
is the first term\r\n" );
document.write( " is the common ratio.\r\n" );
document.write( "Substituting:\r\n" );
document.write( "\r\n" );
document.write( "
is the common ratio.\r\n" );
document.write( "Substituting:\r\n" );
document.write( "\r\n" );
document.write( " \r\n" );
document.write( "\r\n" );
document.write( "Multiply both sides by
\r\n" );
document.write( "\r\n" );
document.write( "Multiply both sides by 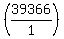 \r\n" );
document.write( "\r\n" );
document.write( "
\r\n" );
document.write( "\r\n" );
document.write( " \r\n" );
document.write( " \r\n" );
document.write( "
\r\n" );
document.write( " \r\n" );
document.write( " \r\n" );
document.write( "\r\n" );
document.write( "Write
\r\n" );
document.write( "\r\n" );
document.write( "Write 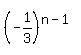 as
as 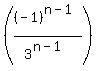 \r\n" );
document.write( "\r\n" );
document.write( "
\r\n" );
document.write( "\r\n" );
document.write( " \r\n" );
document.write( "\r\n" );
document.write( "Multiply both sides by
\r\n" );
document.write( "\r\n" );
document.write( "Multiply both sides by 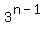 \r\n" );
document.write( "\r\n" );
document.write( "Observe that
\r\n" );
document.write( "\r\n" );
document.write( "Observe that  , so substitute that:\r\n" );
document.write( "\r\n" );
document.write( "
, so substitute that:\r\n" );
document.write( "\r\n" );
document.write( " \r\n" );
document.write( "\r\n" );
document.write( "Divide both sides by
\r\n" );
document.write( "\r\n" );
document.write( "Divide both sides by 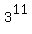 \r\n" );
document.write( "\r\n" );
document.write( "
\r\n" );
document.write( "\r\n" );
document.write( " \r\n" );
document.write( "\r\n" );
document.write( "Subtract exponents on the left:\r\n" );
document.write( "\r\n" );
document.write( "
\r\n" );
document.write( "\r\n" );
document.write( "Subtract exponents on the left:\r\n" );
document.write( "\r\n" );
document.write( " \r\n" );
document.write( "\r\n" );
document.write( "
\r\n" );
document.write( "\r\n" );
document.write( " \r\n" );
document.write( "\r\n" );
document.write( "Since the right side is a power of\r\n" );
document.write( "
\r\n" );
document.write( "\r\n" );
document.write( "Since the right side is a power of\r\n" );
document.write( " , it is either 1 or -1\r\n" );
document.write( "\r\n" );
document.write( "But no power of 3 can be negative, so\r\n" );
document.write( "\r\n" );
document.write( "
, it is either 1 or -1\r\n" );
document.write( "\r\n" );
document.write( "But no power of 3 can be negative, so\r\n" );
document.write( "\r\n" );
document.write( " \r\n" );
document.write( "\r\n" );
document.write( "And since the only power of 3 that gives 1\r\n" );
document.write( "is the 0 power, i.e., 30=1, then\r\n" );
document.write( "the exponent n-12 must equal 0.\r\n" );
document.write( "\r\n" );
document.write( "n-12=0\r\n" );
document.write( " n=12.\r\n" );
document.write( "\r\n" );
document.write( "So there are 12 terms. So \r\n" );
document.write( "\r\n" );
document.write( "
\r\n" );
document.write( "\r\n" );
document.write( "And since the only power of 3 that gives 1\r\n" );
document.write( "is the 0 power, i.e., 30=1, then\r\n" );
document.write( "the exponent n-12 must equal 0.\r\n" );
document.write( "\r\n" );
document.write( "n-12=0\r\n" );
document.write( " n=12.\r\n" );
document.write( "\r\n" );
document.write( "So there are 12 terms. So \r\n" );
document.write( "\r\n" );
document.write( " \r\n" );
document.write( "\r\n" );
document.write( "becomes:\r\n" );
document.write( "\r\n" );
document.write( "
\r\n" );
document.write( "\r\n" );
document.write( "becomes:\r\n" );
document.write( "\r\n" );
document.write( " \r\n" );
document.write( "\r\n" );
document.write( "write
\r\n" );
document.write( "\r\n" );
document.write( "write 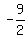 as
as  \r\n" );
document.write( "\r\n" );
document.write( "
\r\n" );
document.write( "\r\n" );
document.write( " \r\n" );
document.write( "\r\n" );
document.write( "write
\r\n" );
document.write( "\r\n" );
document.write( "write 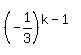 as
as 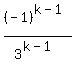 \r\n" );
document.write( "\r\n" );
document.write( "
\r\n" );
document.write( "\r\n" );
document.write( " \r\n" );
document.write( "\r\n" );
document.write( "Write
\r\n" );
document.write( "\r\n" );
document.write( "Write  as
as  :\r\n" );
document.write( "\r\n" );
document.write( "
:\r\n" );
document.write( "\r\n" );
document.write( " \r\n" );
document.write( "\r\n" );
document.write( "
\r\n" );
document.write( "\r\n" );
document.write( " \r\n" );
document.write( "\r\n" );
document.write( "
\r\n" );
document.write( "\r\n" );
document.write( " \r\n" );
document.write( "\r\n" );
document.write( "Add exponents of
\r\n" );
document.write( "\r\n" );
document.write( "Add exponents of  on top:\r\n" );
document.write( "\r\n" );
document.write( "
on top:\r\n" );
document.write( "\r\n" );
document.write( " \r\n" );
document.write( "\r\n" );
document.write( "
\r\n" );
document.write( "\r\n" );
document.write( " \r\n" );
document.write( "\r\n" );
document.write( "Subtract exponents of 3:\r\n" );
document.write( "\r\n" );
document.write( "
\r\n" );
document.write( "\r\n" );
document.write( "Subtract exponents of 3:\r\n" );
document.write( "\r\n" );
document.write( " \r\n" );
document.write( "\r\n" );
document.write( "
\r\n" );
document.write( "\r\n" );
document.write( " \r\n" );
document.write( "\r\n" );
document.write( "Edwin
\r\n" );
document.write( "\r\n" );
document.write( "Edwin
\n" );
document.write( "
