Question 971429: A takes 45 seconds to run a lap and every 25 seconds, B who is running in the opposite direction passes A. how long does it take B to run a lap?
Found 2 solutions by Theo, anand429:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! A takes 45 seconds to do a lap.
B passes A every 25 seconds.
if you look at the first lap only, B will pass A after 25 seconds have elapsed.
this means that A has run 25/45 of the lap while B has only run 20/45 of the lap.
B has to be running slower than A.
the ratio of B's speed to A's speed is therefore 20/45 divided by 25/45 = 20/25 = 4/5.
B is running at 4/5 the speed of A.
rate * time = distance.
time for A is 45 seconds.
distance for A is 1 lap.
rate for A is determined by the equation of r*t = d which becomes r*45 = 1 which becomes 1/45.
the rate of A is 1/45.
the rate of B is only 4/5 that, so the rate of B has to be 4/5 * 1/45 = 4/225.
the rate of B is 4/225.
rate * time = distance.
4/225 * t = 1
t = 225/4 = 56.25 seconds.
A takes 45 seconds.
B takes 56.25 seconds.
it's really hard to show but i think it's correct.
let's assume that A is running at 5 yards a second and B is running at 4 yards a second.
A will run 1 lap in 45 seconds which is equal to 5*45 = 225 yards.
B will run 1 lap in 56.25 seconds which is equal to 4 * 56.25 = 225 yards.
so one lap is equal to 225 yards.
we'll look at the position around the track of A and B every 25 seconds.
in 25 seconds, A will be at the 25/45 * 225 = 125 yard mark.
in the same 25 seconds, B will be at the 25/56.25 * 225 = 100 yard mark.
since A is running in the opposite direction from B, then B is at the 225 - 100 = 125 yard mark of A.
in other words, they pass each other at the 25 second mark.
in 50 seconds, A will be at the 50/45 * 225 = 250 yard mark.
since the track is only 225 yards, then A has done 1 lap and is at the 25 yard mark of his second lap.
in the same 50 seconds, B will be at the 50/56.25 * 225 = 200 yard mark of his first lap.
since they are traveling in opposite directions, B's 200 yard mark is really A's 25 yard mark, so they pass each other again.
in 75 seconds, A will be at the 75/45 * 225 = 375 yard mark.
since the track is only 225 yards, then A is at the 375 - 225 = 150 yard mark of his second lap.
in the same 75 seconds, B will be at the 75/56.25 * 225 = 300 yard mark.
since the track is only 225 yards, then B is at the 300 - 225 = 75 yard mark of his second lap.
since B is traveling in the opposite direction as A, then B's 75 yard mark is really A's 225 - 75 = 150 yard mark.
they are passing each other again at A's 150 yard mark.
this continues and repeats every 25 seconds.
we can go on forever, but we should be able to see that they will pass each other every 25 seconds.
take any 25 second periods and you will see that they are at the same position relative to each other.
for example:
assume that 300 seconds have elapsed.
A will have traveled 300/45 * 225 = 1500 yards.
since the track is only 225 yards, then A is at his 150 yard mark in his seventh lap. 6 laps is 6 * 225 = 1350 yards + 150 = 1500 yards.
B will have traveled 300/56.25 * 225 = 1200 yards.
since the track is only 225 yards, then B is at his 75 yard mark in his 6th lap.
5 laps is 5 * 225 = 1125 yards + 75 = 1200 yards.
since B is running in the opposit3e direction from A, then he is at the 225 - 75 = 150 yards mark of A.
they are at the same position in the track after 300 seconds which means they are just passing each other again.
i believe your solution is that it will take B 56.25 seconds to complete one lap.
he is running at 4/5 the speed that A is running at.
it took him 25 seconds to run the same distance that it took A 20 seconds to run.
Answer by anand429(138)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let A's speed be a m/sec and B's be b m/sec, and lap length be l,
Then for A,  -(i) -(i)
In 25seconds,
Distance covered by A = 25*a and
Distance covered by B = 25*b
Since both meet every 25 seconds,
So, both combinedly cover the distance equivalant of 1 lap,
So, 
Putting value of a from eqn (i),
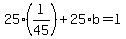
=> 
=> 
=> 
=> 
So, time taken by B to run a lap = lap length/B's speed
= l/b
= 225/4 seconds
|
|
|