Question 133921: Hi The chapter im working on is called Rational Functions. I got this word problem in my homework and did not now how to solve it at all.
Heres the problem
4. The speed of the current in a river is 5 miles per hour. A boat leaves a dock on the bank of the river, travels upstream 25 miles, and returns to the dock in 12 hours. What is the speed of the boat in still water?
Maybe you could help? Thank you
Answer by solver91311(24713)   (Show Source):
You can put this solution on YOUR website! Rate of the boat in still water (the thing we want to determine): 
The time it takes for the boat to go upstream: 
The time it takes for the boat to go downstream: 
The speed of the current: 
The distance traveled:  each way.
When the boat is going upstream, it's rate relative to the shoreline is the rate of the boat in still water MINUS the rate of the current:  .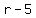
Likewise, when the boat is going downstream, the rate relative to the shoreline is:  .
Using the relationship  , we can write an equation for the upstream trip thusly:
And we can write an equation for the downstream trip:
However, we are given that the entire trip took 12 hours, so we know that  , which can be written 
Using this information we can re-write the equation for the upstream trip by substitution:
Beginning with the equation for the downstream trip, solve for :
And then solve the last form of the equation for the upstream trip for
Now we have two different expressions in terms of the rate of the boat in still water, , that are equal to the time for the downstream trip , so set these two expressions to be equal to each other:
Simplify and isolate
Need a common denominator, which would be  , so:
Distribute and collect like terms:
Since we know that  if and only if  and 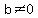 , all we have to do is set the numerator equal to 0 and solve, excluding any root that would make the denominator go to zero, namely 5 and -5, and also excluding any root that is negative because a negative value for time would make no sense.
We can take out a factor of -2 to make the coefficients a little more manageable:
Very conveniently, this quadradic is factorable: (How did I know that? I used an on-line quadratic solver -- there are a number of them available -- and noted that the roots were rational numbers. I just worked backwards from the roots given by the solver to get the factors)
Therefore:
 or 
Neither root is 5 or -5, but the second one is negative and can be excluded. The one acceptable solution is mph.
Check the answer:
The boat went upstream for 25 miles at  mph, so the trip took  hours.
The boat went downstream for 25 miles at  mph, so the return trip took  hours.
 Answer checks.
|
|
|
