SOLUTION: In​ 2012, the population of a city was 5.62 million. The exponential growth rate was ​2.41% per year. ​a) Find the exponential growth function. ​b) Estimate the populatio

Algebra.Com
Question 1198714: In​ 2012, the population of a city was 5.62 million. The exponential growth rate was ​2.41% per year.
​a) Find the exponential growth function.
​b) Estimate the population of the city in 2018.
​c) When will the population of the city be 9million?
​d) Find the doubling time.
I already asked this question but I need more Clarification
Found 2 solutions by Theo, josgarithmetic:
Answer by Theo(13342)   (Show Source): You can put this solution on YOUR website!
the formula to use is f = p * (1+r) ^ n
f is the future value
p is the present value
r is the growth rate per time period
(1+r) is the growth factor per time period
n is the number of time periods
p is equal to 5.62
r is equal to 2.41% / 100 = .0241
1+r is equal to 1.0241
n is equal to 2018 minus 2012 = 6
formula becomes f = 5.62 * (1+r) ^ 6
solve for f to get f = 6.483216317.
answer to (a) ia f = p * (1+r) ^ n
answer to (b) is 6.483216317
answers to c and d are shown below.
c) When will the population of the city be 9 million?
to find this, replace f with 9 in the equation to solve for b and replace 6 with n to get:
9 = 5.62 * 1.0241 ^ n
divide both sides of the equation by 5.62 to get:
9/5.62 = 1.0241 ^ n
take the natural log of both sides of the equation to get:
ln(9/5.62) = ln(1.0241 ^ n)
since ln(1.0241 ^ n) = n * ln(.0241), the equation becomes:
ln(9/5.62) = n * ln(1.0241)
divide both sides of the equation by ln(1.0241) to get:
ln(9/5.62) / ln(1.0241) = n
solve for n to get:
n = 19.77363701
to confirm, replace n in the equation with that and solve for f to get:
f = 5.62 * 1.0241 ^ 19.77363701 = 9, confirming the value of n is correct.
since your base year is 2012, add 19.7763701 to that to get 2031.773637.
that should be in the year sometime in the year 2031.
​d) Find the doubling time.
to find the doubling time, multiply 5.62 * 2 to get 11.24
equation becomes 11.24 = 5.62 * 1.0241 ^ n
divide both sides of the equation by 5.62 to get:
2 = 1.0241 ^ n
take natural log of both sides of the equation to get:
ln(2) = ln(1.0241^n)
since ln(1.0241^n) is equal to n * ln(1.0241), equation becomes:
ln(2) = n * ln(1.0241)
divide both sides of the equation by ln(1.0241) and solve for n to get:
n = ln(2) / ln(1.0241) = 29.10649184
that's the number of years it will take for 5.62 to double.
confirm by replacing n with that in the equation and solving for f to get:
f = 5.62 * 1.0241 ^ 29.20619184 = 11.24, confirming the value of n is good.
your solution is that it will take 29.20619184 years for the population to double.

the equation can be graphed as shown below:


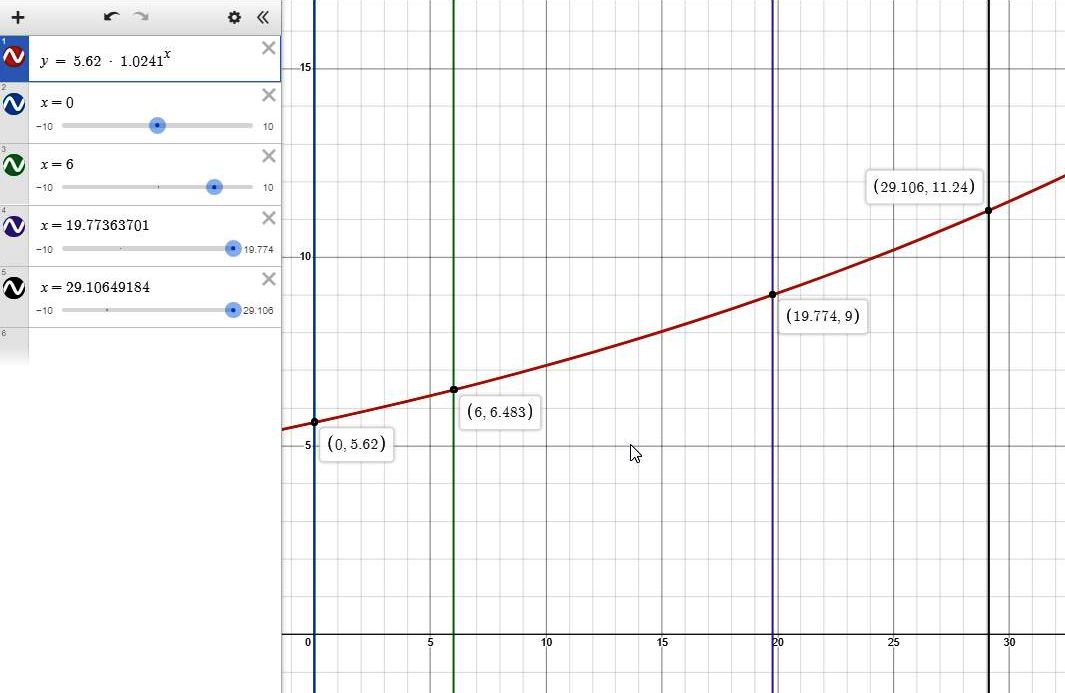
i'm not sure if this is going to help you, but i thought i would give it a try.
let me know if you have any questions.
theo

Answer by josgarithmetic(39613)   (Show Source): You can put this solution on YOUR website!
The factor is 1.0241 every year.
Time x=0 for year 2012.


The Doubling-Time




------Doubling Time in years; about 29 years 5 and a half weeks
RELATED QUESTIONS

In 2012 , the population of a city of was 5.75 million. The exponential growth rate... (answered by Alan3354)
In​ 2012, the population of a city was 5.82 million. The exponential growth rate was... (answered by Boreal)
In​ 2012, the population of a city was 5.21 million. The exponential growth rate... (answered by Theo,ankor@dixie-net.com)
In​ 2012, the population of a city was 6.97 million. The exponential growth rate was... (answered by Shin123)
In 1998, the population of a given country was 37 million, and the exponential growth... (answered by nerdybill)
In 1998, the population of a given country was 37 million, and the exponential growth... (answered by checkley77)
In​ 2012, the population of a city was 5.72 million. The exponential growth rate... (answered by stanbon)
In 1980, the population of a city was 6.8 million. By 1992 the population had grown to... (answered by stanbon)
The population of a city was 127 thousand in 1992. The exponential growth rate was 1.3%... (answered by nerdybill)