Question 1148210: Stu trained for a triathlon for 5 hours yesterday. He ran 5 miles and then biked 80 miles. His biking speed is 15 mph faster than his running speed. What is his running speed?
Answer by ikleyn(52863)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Based on the given data, I can guess the answer in 5 seconds.
His running speed is 5 miles per hour.
CHECK. He spent 1 hour running and 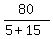 = 4 hours biking. = 4 hours biking.
But if you want ALGEBRA solution, here it is.
Let x be the running speed, which is the value under the question.
Then his biking speed is (x+15) miles per hour.
The time spent running is 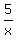 hours.
The time spent biking is hours.
The time spent biking is 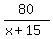 .
The total time is 5 hours; it gives you and equation .
The total time is 5 hours; it gives you and equation
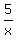 + + 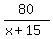 = 5 hours.
It is so called "time" equation.
As soon as you got it, the setup is just completed.
Now your task is to solve it.
For it, multiply both sides by x*(x+15). You will get
5*(x+15) + 80x = 5x*(x+15)
(x+15) + 16x = x*(x+15)
17x + 15 = x^2 + 15x
x^2 - 2x - 15 = 0
(x-5)*(x+3) = 0
Of the two roots, x= 5 and x= -3, only positive x= 5 makes sense.
So, your answer is: the running speed is 5 mph; same as I guessed at the beginning. = 5 hours.
It is so called "time" equation.
As soon as you got it, the setup is just completed.
Now your task is to solve it.
For it, multiply both sides by x*(x+15). You will get
5*(x+15) + 80x = 5x*(x+15)
(x+15) + 16x = x*(x+15)
17x + 15 = x^2 + 15x
x^2 - 2x - 15 = 0
(x-5)*(x+3) = 0
Of the two roots, x= 5 and x= -3, only positive x= 5 makes sense.
So, your answer is: the running speed is 5 mph; same as I guessed at the beginning.
Solved.
-----------------------
Using "time" equation is the STANDARD method of solving such problems.
From this lesson, learn on how to write, how to use and how to solve a "time" equation.
To see many other similar solved problems, look into the lessons
- Had a car move faster it would arrive sooner
- How far do you live from school?
- Earthquake waves
- Time equation: HOW TO use, HOW TO write and HOW TO solve it
in this site.
|
|
|