.
1 - One-line solution, Physics style
The distance under the question is  = 17*2 = 34 miles.
= 17*2 = 34 miles.
2 - One-line solution, Physics style with more explanations
The distance under the question is  = 17*2 = 34 miles.
= 17*2 = 34 miles.
Explanations.
17+83 = 100 mph in the denominator is the relative speed of the participants, i.e. the rate of decreasing the distance between them.
 =
= 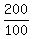 = 2 hours is the time before they meet.
Thus
= 2 hours is the time before they meet.
Thus  is "at what distance from point A will they meet".
is "at what distance from point A will they meet".
3 - Algebra style solution using equation
The equation is
17*t + 83*t = 200,
which says that the sum of the distances each participant covers before they meet is equal to the total initial distance of 200 miles.
From the equation,
t =  is the time to get the meeting point.
Hence,
is the time to get the meeting point.
Hence,  is the distance from the point A which the cyclist will cover when they meet each other,
exactly as it was explained in Solutions 1 and 2.
is the distance from the point A which the cyclist will cover when they meet each other,
exactly as it was explained in Solutions 1 and 2.
-------------
For the introductory lessons on Travel and Distance see the lessons
- Travel and Distance problems
- Travel and Distance problems for two bodies moving in opposite directions
- Travel and Distance problems for two bodies moving in the same direction (catching up)
in this site.