Question 1014984: Hello, could you please help me with this word problem: In 1971, Apollo 14 astronaut Alan Shepard hit to golf balls on the moon. A golf enthusiasts of the future decides to play golf on many worlds throughout the solar system, and hits the golf ball consistently at an angle of 45° and a speed of 144 feet per second. The path of the golf ball can be modeled by the quadratic equation: y=- g/20736 x^2+x where X is the balls horizontal position (in feet) and G is its corresponding height (in feet) and she is the acceleration due to gravity (in feet per second squared).
What is the horizontal distance traveled by the golf ball on the moon, where G=5.32 and what is the maximum height of the golf ball on Mars, where G=12.17?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The path of the golf ball can be modeled by the quadratic equation
 , where , where
 is the ball's horizontal position (in feet), is the ball's horizontal position (in feet),
 is its corresponding height (in feet), and is its corresponding height (in feet), and
 is the acceleration due to gravity (in is the acceleration due to gravity (in 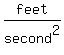 ). ).
On the moon,  , so the ball is an the moon's surface, at , so the ball is an the moon's surface, at  when when
 --> --> --> --> --> -->
There are two moments when the ball is on the moon's surface:
 (when the ball is hit and has not traveled horizontally), and (when the ball is hit and has not traveled horizontally), and
 , when the ball hits the moon's surface after travelling a horizontal distance of about , when the ball hits the moon's surface after travelling a horizontal distance of about  (rounded). (rounded).
When the golf ball is hit on Mars, where   , ,
the path of the golf ball can be modeled by the quadratic equation
 , where , where
 is the ball's horizontal position (in feet), and is the ball's horizontal position (in feet), and
 is its corresponding height (in feet). is its corresponding height (in feet).
That equation represents a parabola
Your teacher wants you to remember that a quadratic function 
with 
represents a parabola with a vertex/maximum at
 , ,
so you could apply that "formula" with  and and  , ,
and then you could substitute the  value found into value found into  to find the maximum height, to find the maximum height,
 . .
Alternately, you could "complete the square":





So,  --> --> --> --> } . } .
So, in Mars, the ball reaches a height of  . .
|
|
|