time = distance / rate
a.
t(v) = time as a function of v.
v = number of miles per hour traveled above the state speed limit.
270 is the distance in state A.
405 is the distnace in state B.
50 is the speed limit in state A.
55 is the speed limit in state B.
b.
solve for t(v) to get t(v) = 12.29757085 hours.
c.
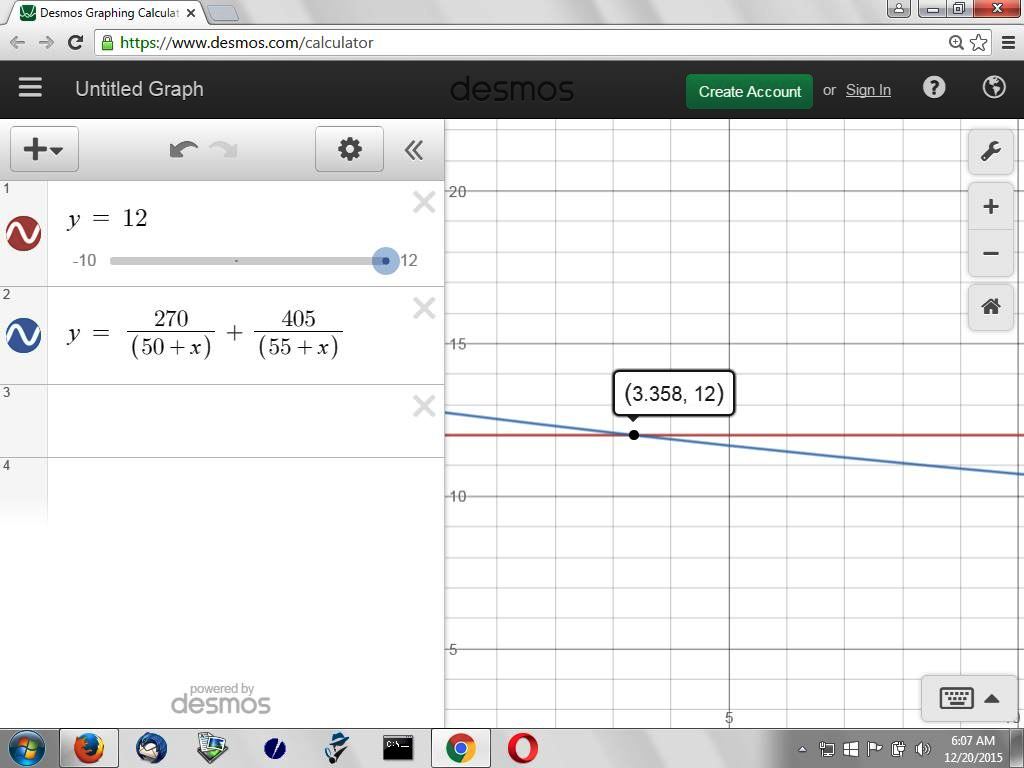
if you have a graphing calculator, then you can solve this easily by graphing y = 12 and y = 270/(50+x) + 405/(55+x) and then looking for the intersection of the graph of both those equations.
you can also solve it algebraically, but graphing so much easier if you have the right graphing tool.
i used a ti-84 plus.
there is also an online calculator at www.desmos.com/calculator that can do it as well.
i got x = 3.358384665 using the ti-84 plus.
the graphing calculator gave me a more rounded answer as shown below:
you can also solve this algebraically by converting the equation into ax^2 + bx + c = 0 form and then using the quadratic formula to solve for x.
start with
multiply both sides of this equation by
multiply all the factors and subtract the right side of the equation from both sides of the equation and you will get
put this in the form of
negative values of x are no good so the solution is x = 3.358384665.
you could have accessed the table of values but that's a laborious process and unnecessary when the graphing software tells you the answer directly from the graph.
if you solved using the quadratic formula, you would have gotten the same answer.
the equation would be
since it is in standard form of ax^2 + bx + c = 0, then:
a = 12
b = 585
c = -2100
the quadratic formuls is:
x = -b plus or minus sqrt(b^2-4ac)
------------------------------
2a
replace b with 585 and a with 12 and c with -2100 and you get:
x = -585 plus or minus sqrt(585^2-4*12*-2100)
------------------------------
(2*12)
all you have to do now is evaluate the equation to get the value of x.
the graph of the equation
