|
Question 665192: Ten consectutive integers greater than 5 billion are each raised to the fifth power, the new numbers are then added together. what is the ones digit of the sum?
Answer by kevwill(135)   (Show Source): (Show Source):
You can put this solution on YOUR website! Don't be fooled by the "greater than 5 billion" in the problem statement. The only thing that matters is the ones digit.
Think of it this way: Every integer can be expressed as the sum of a multiple of 10 and a single digit (e.g. for any integer x, x = 10k + i where 0 <= i <= 9). So,


Note that every term is multiple of 10 except 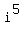 , so the ones digit of , so the ones digit of 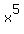 is the same as the ones digit of is the same as the ones digit of 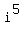 . That is . That is
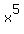 mod 10 = mod 10 = 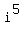 mod 10}}} mod 10}}}
So any 10 consecutive integers will have ones digits of 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9 (not necessarily in that order). Raising each of those integers to the 5th power will result in numbers with ones digits equal to the ones digits of  , again, not necessarily in that order. , again, not necessarily in that order.
So all we need to know is:
 mod 10 = 0 mod 10 = 0 mod 10 = 0 mod 10 = 0
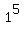 mod 10 = 1 mod 10 = 1 mod 10 = 1 mod 10 = 1
 mod 10 = 32 mod 10 = 2 mod 10 = 32 mod 10 = 2
 mod 10 = 243 mod 10 = 3 mod 10 = 243 mod 10 = 3
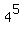 mod 10 = 1024 mod 10 = 4 mod 10 = 1024 mod 10 = 4
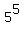 mod 10 = 3125 mod 10 = 5 mod 10 = 3125 mod 10 = 5
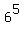 mod 10 = 7776 mod 10 = 6 mod 10 = 7776 mod 10 = 6
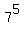 mod 10 = 16807 mod 10 = 7 mod 10 = 16807 mod 10 = 7
 mod 10 = 32768 mod 10 = 8 mod 10 = 32768 mod 10 = 8
 mod 10 = 59049 mod 10 = 9 mod 10 = 59049 mod 10 = 9
So the ones digit we are looking for is
(0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9) mod 10 = 45 mod 10 = 5
The ones digit of the sum is 5.
|
|
|
| |