I will assume by "number" you mean positive integer.
Break 84 into its prime factors.
84 = 2*2*3*7
I. First we will get all possible 4 digit integers with product of digits 84:
A. Any 4 digit permutation of the digits 2,2,3,7 will have product 84
There are 2 indistinguishable digits, so the number of distinguishable
permutations of those is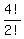 
= 
= 12
B. We can multiply factors 2*2 and get the digit 4 and introduce 1 to
get 4-digit integers with digits 4,3,7,1
There are 4! or 24 permutations of these
C. We can multiply factors 2*3 and get the digit 6 and introduce 1 to
get 4-digit integers with digits 6,2,7,1
There are 4! or 24 permutations of these
So there are 12+24+24 = 60 four-digit integers with product of digits 84.
II. Next we will get all possible 3-digit integers with product of digits 84.
A. We can multiply factors 2*2 and get the digit 4. So any three-digit
integer with digits 4,3,7 will have product of digits 84
There are 3! or 6 permutations of these
B. We can multiply factors 2*3 and get the digit 6.
So any three-digit integers with digits 6,2,7
There are 3! or 6 permutations of these
So there are 6+6 = 12 three-digit integers with product of digits 84
III. There are no 2-digit integers with product of digits 84, since the
largest product of digits is for 99, which has product of digits of
only 81.
Answer: 60 four-digit integers and 12 three-digit integers.
Total 72.
[Note: If you actually mean numbers, and not just integers, you would have
to count each four-digit number like, say, 2347 five times, as
.2345, 2.347, 23.47, 234.7, and 2347. So there would be 60×5 or 300 four
digit numbers. Also each 3-digit number like , say, 437 four times, as
.437, 4.37, 43.7, and 437. So there would be 12×4 or 48 three-digit numbers.
And in that case the total number would be 348. However I believe you
meant just integers.]
Edwin
