|
Question 621382: Please help me to solve this question:
Prove that the product of two consecutive odd integers is always 1 less than a multiple of 4.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Usually, for problems with consecutive odd numbers, it is enough to call them n and n+2, and the same goes with consecutive even numbers.
In this case, we have to express the numbers in a way that shows they are odd.
To specify that a number is even, we can call it 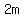 and specify that m is a positive integer, so the even number could be 2, 4, 6, etc. and specify that m is a positive integer, so the even number could be 2, 4, 6, etc.
The numbers right before and right after an even number are consecutive odd integers, so we will use  and and 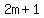 as our consecutive odd integers. as our consecutive odd integers.
Any pair of consecutive odd integers can be expressed as  and and 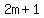 . .
For any pair of consecutive odd integers we can find their m by calculating their average (the even number between them) and dividing by 2.
The product of  and and 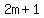 is is

Since  was a positive integer, was a positive integer, 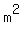 is a positive integer and is a positive integer and
 is a multiple of 4. is a multiple of 4.
 is one less than is one less than 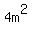 , so it is 1 less than a multiple of 4. , so it is 1 less than a multiple of 4.
|
|
|
| |