|
Question 482623: the sum of the digits of a two digit number is 15.if the number formed by reversing the digits is less than the original number by 27.find the original number
Found 2 solutions by cleomenius, MathTherapy:
Answer by cleomenius(959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Maybe there is a better way to do this, but I found the combinations of single digit numbers that would equal 15; they came to 6,9 and 8,7.
the number 96 fits the critera, 86 -27 = 69.
Cleomenius.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the tens digit be T, and the units digit U
As sum of digits = 15, then T + U = 15
The value of this number is: 10(T) + U. or 10T + U, and when reversed, we have: 10(U) + T, or 10U + T
Since the # formed by reversing the digits is 27 less than the original number, then we can say that:
10U + T = 10T + U – 27 --------> – 9T + 9U = -27
We now have the following simultaneous equations:
T + U = 15 _____ (i)
– 9T + 9U = - 27 _____ (ii)
9T + 9U = 135 _______ (iii) ----- Multiplying eq (i) by 9
18U = 108 _______ Adding eq (ii) and eq (iii)
U, or the units digit = 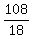 , or , or 
Substituting 6 for U in eq (i), we get: T + 6 = 15 ----- T, or the tens digit = 
Now, since the tens digit is 9, and the units digit is 6, this makes the number: 
----------
Check
----------
When 96 (original #) is reversed, it becomes 69. 69 is in fact 27 less than 96 (96 - 69 = 27).
Send comments and “thank-yous” to MathMadEzy@aol.com
|
|
|
| |