Question 1186692: How many different integers can be represented as a sum of four distinct numbers chosen from the set (5,9,13,17,…,49)
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
How many different integers can be represented as a sum of four distinct numbers chosen from the set (5,9,13,17,…,49)
~~~~~~~~~~~~~~~~
The given set represents the terms of the arithmetic progression with the first term of 5 and the common difference of 4:
 = 5 + 4m, m = 0, 1, 2, 3, . . . , 11.
In all, the set has 12 elements.
The sum of any 4 numbers of the set is the number of the form = 5 + 4m, m = 0, 1, 2, 3, . . . , 11.
In all, the set has 12 elements.
The sum of any 4 numbers of the set is the number of the form 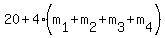 ,
where ,
where 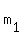 , ,  , , 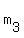 and and 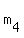 are different integer numbers between 0 and 11, inclusive.
The minimum value of such sum are different integer numbers between 0 and 11, inclusive.
The minimum value of such sum 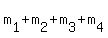 is, OBVIOUSLY, 0+1+2+3 = 6.
The maximum value of such sum is, OBVIOUSLY, 0+1+2+3 = 6.
The maximum value of such sum 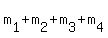 is, OBVIOUSLY, 8+9+10+11 = 38.
It is clear that any index from 6 to 38 can be obtained as the sum of this form is, OBVIOUSLY, 8+9+10+11 = 38.
It is clear that any index from 6 to 38 can be obtained as the sum of this form 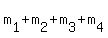 .
THEREFORE, the ANSWER to the problem's question is 38 - 6 + 1 = 33. .
THEREFORE, the ANSWER to the problem's question is 38 - 6 + 1 = 33.
Solved.
|
|
|