|
Question 1129189: Find 3 consecutive Integers whose some is 195
Found 3 solutions by MathLover1, josmiceli, greenestamps:
Answer by MathLover1(20850)   (Show Source):
Answer by josmiceli(19441)  (Show Source):
Answer by greenestamps(13203)  (Show Source):
You can put this solution on YOUR website!
Both of the other two tutors used n, n+1, and n+2 (or x, x+1, and x+2) for the three consecutive integers. If you are going to solve the problem with formal algebra, it is often easier (as in this case) to let the three integers be x-1, x, and x+1. Then the algebra is a bit easier:
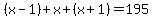
The three integers are x-1=64, x=65, and x+1=66.
In this particular problem, using x-1, x, and x+1 for three consecutive integers only made the problem a bit easier to solve. But in more complicated problems involving consecutive integers, it can make a big difference in the amount of work required to solve the problem.
But note that this problem can be solved using informal logical reasoning MUCH faster than with formal algebra. The exact same calculations are used; but you aren't slowed down with defining variables and solving equations.
In any 3 consecutive integers, the middle one is the average of all three. Since the sum is 195, the average is 195/3 = 65; then the 3 integers are 64, 65, and 66.
|
|
|
| |
