|
Question 1116378: How many integers between 1 and 100 can be written as the difference of two perfect squares?
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
We are looking to find all the numbers from 1 to 100 that can be written in the form

where a and b are positive integers with a>b.
(1) If a = b+1, then

Since b is any positive integer, this means every odd number except 1 can be written as the difference of two squares.
As an example, if the number is 31, then
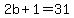
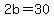

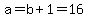
and

So we know that all odd numbers except 1 can be written as the difference of perfect squares.
There are 50 odd numbers from 1 to 100; all but one of them can be written as the difference of perfect squares.
So at this point we have found 49 numbers from 1 to 100 that can be written as the difference of perfect squares.
(2) So what even numbers can be written as the difference of perfect squares?
To get an even difference of perfect squares a^2 and b^2, a and b must be either both even or both odd. In either case, the difference of squares is a multiple of 4. So we know that the only even numbers that can be written as the difference of perfect squares are those that are divisible by 4.
There are 50 even numbers from 1 to 100; half of them are divisible by 4, the other half are not. So we have found 25 even numbers from 1 to 100 that can NOT be written as the difference of perfect squares.
Finally, similar to the case for odd numbers, not ALL multiples of 4 can be written as the difference of perfect squares.
If a = b+2, then

Since b has to be a positive integer, the smallest multiple of 4 that CAN be written as the difference of perfect squares is 8 (when b=1).
So we have the answer to the question. The numbers from 1 to 100 that CAN be written as the difference of perfect squares are
(1) all odd numbers except 1 (49 numbers); and
(2) all multiples of 4 except 4 (24 numbers)
making a total of 73.
|
|
|
| |