SOLUTION: Four lines on a plane have at most N common points. FIND N. A)7 B)6 C)5 D)4

Algebra ->  Customizable Word Problem Solvers  -> Mixtures -> SOLUTION: Four lines on a plane have at most N common points. FIND N. A)7 B)6 C)5 D)4      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1143914: Four lines on a plane have at most N common points. FIND N.
A)7
B)6
C)5
D)4
Found 3 solutions by MathLover1, Alan3354, ikleyn:
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!

First, you have 2 straight lines. They would have at most one common point.
Next, add one more line. This new line can intersect both existing lines, adding 2 points to the set of common points.
Finally, add one more line. This new line can intersect all existing 3 lines, adding 3 points to the set of common points.
So in total, we have 6.
answer:
B) 6

Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
Four lines on a plane have at most N common points. FIND N.
===========
Not a well posed problem.
---
If 2 or more or the lines are coincident, N = an infinite number.
Not more than that.

Answer by ikleyn(52797) About Me  (Show Source):
You can put this solution on YOUR website!
.

            More accurate formulation is THIS : 

                Four highlight%28distinct%29 lines on a plane have at most N common points. FIND N.


Solution 

    Two distinct straight lines may have at most 1 common point (the intersection point).


    So the maximum number of common points of " n " lines is equal to the number of all pairs of lines of the given set of lines.


    More exactly, the maximum number of common points of N lines is equal to the number of all unordered pairs of lines of the given set of lines.


    In other words, the maximum number of common points of N lines is equal to the number of all combinations 
    of given lines taken 2 at a time  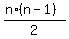C%5Bn%5D%5E2 = %28n%2A%28n-1%29%29%2F2.


    In case n = 4, the maximum number of common points of  lines is  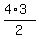%284%2A%284-1%29%29%2F2 = %284%2A3%29%2F2 = 2*3 = 6.


    This maximum number is achieved if and only if any two lines from the set intersect each other, i.e. are not parallel.


Solved, explained, answered and completed.


/\/\/\/\/\/\/\/

I will give a BONUS problem to you to develop your mind. 

    Find the maximum possible number of intersection points that N circles may have on a plane ?

If you understand my solution to the previous problem, you should be able to solve this one, too.

-------------------

On Combinations,  see introductory lessons
    - Introduction to Combinations
    - PROOF of the formula on the number of Combinations
    - Problems on Combinations
    - OVERVIEW of lessons on Permutations and Combinations
in this site.

Also,  you have this free of charge online textbook in ALGEBRA-II in this site
    - ALGEBRA-II - YOUR ONLINE TEXTBOOK.

The referred lessons are the part of this online textbook under the topic  "Combinatorics: Combinations and permutations".


Save the link to this textbook together with its description

Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson

into your archive and use when it is needed.