Question 1204315: A three-digit number ABC is divided by the two-digit number AC. The quotient is 11 with no remainder. What is the largest possible number ABC?
Found 4 solutions by math_tutor2020, MathLover1, ikleyn, greenestamps:
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The three digit number ABC means
A = hundreds digit
B = tens digit
C = units or ones digit
ABC is more formally written as 100A+10B+C
AC becomes 10A+C
Divide those values and we get a quotient of 11 and no remainder.
(100A+10B+C)/(10A+C) = 11
100A+10B+C = 11(10A+C)
100A+10B+C = (10+1)(10A+C)
100A+10B+C = 10(10A+C)+1(10A+C)
100A+10B+C = 100A+10C+10A+C
10B+C = 10C+10A+C
10B = 10C+10A
0 = 10A-10B+10C
10(A-B+C) = 0
A-B+C = 0
A = B-C
To make number ABC as large as possible, we need A as large as possible.
At the same time, we need B to be as large as possible as well.
For unique single digits B and C, B-C maxes out when these digits are as far away from each other as possible, and when B > C.
That happens when B = 9 and C = 0
So A = B-C = 9-0 = 9
But A = 9 and B = 9 overlap.
We assume that A and B are different values. Otherwise the number ABC would be AAC or BBC.
Let's go for B = 9 and C = 1 instead.
A = B-C = 9-1 = 8
This would allow A,B,C to be different integers.
The number ABC = 891 is the largest possible value so that ABC/AC = 11 without a remainder (i.e. remainder is 0).
More specifically,
891/81 = 11
Answer: 891
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
write a three-digit number  as: as:

and the number  (divisor) is: (divisor) is:

We know that  with no remainder, with no remainder,

or


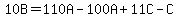

Remember that  , ,  , ,  , being digits of an integer number, must be whole numbers between , being digits of an integer number, must be whole numbers between  and and  , and that , and that  isn’t zero. isn’t zero.
 must be not must be not  as well, otherwise as well, otherwise 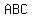 would have only two digits and not three. would have only two digits and not three.
as you can see, 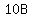 , ,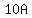 , and , and 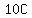 are a multiple of are a multiple of  . .
It’s easy to verify that the only value of  that satisfies this condition is that satisfies this condition is  ; all other values for ; all other values for  between between  and and  yield a value for yield a value for 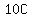 that is not divisible by that is not divisible by  . .
Thus, if  , we can replace , we can replace  for for  and write: and write:

dividing both terms by  : :

The only values that satisfy that condition are:


. Let’s summarize:



then


check:

In fact,  with no remainder. with no remainder.
Answer by ikleyn(52878)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The @MathLover1 "solution" is one-to-one copy-paste from this web-page,
https://www.quora.com/A-three-digit-number-ABC-is-divided-by-the-two-digit-number-AC-The-quotient-is-13-with-no-remainder-What-is-the-number-ABC-if-c-0
with no reference, naturally.
Answer by greenestamps(13209)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Although a formal algebraic solution is good, and the student should be able to understand it, a very different and much easier path to the answer is possible.
Given that the 3-digit number ABC divided by the 2-digit number AC gives a quotient of 11 with no remainder, we know that AC*11 = ABC. So look at that multiplication in the way we learn multiplication in grade school.
A C
X 1 1
------
A C
A C
-------
A B C
The problem asks for the largest possible value of the 3-digit number ABC. So let's see if the condition can be satisfied if A is 9.
9 C
X 1 1
------
9 C
9 C
-------
9 B C
We can see that with A = 9, C must be 0, giving us
9 0
X 1 1
------
9 0
9 0
-------
9 9 0
So A = B = 9 and C = 0. Generally, in problems like this, it is specified that different letters represent different digits. However, that is not specified in the statement of this problem. So the answer could be
ANSWER: ABC = 990
Assuming any information that is not given in a problem is never good mathematics. However, if we assume that the letters represent different digits, then A = 9 doesn't work. So again looking for the largest possible value of the 3-digit number ABC, we try A = 8:
8 C
X 1 1
------
8 C
8 C
-------
8 B C
Here we can see that B can be at most 9, which means C can be at most 1. And since we want ABC to be the largest possible, we choose C = 1, giving us
8 1
X 1 1
------
8 1
8 1
-------
8 9 1
And in this case we have
ANSWER: ABC = 891
----------------------------------------------------------------------
And then here is another solution VERY different from the others, and MUCH faster.
Using the divisibility rule for 11 in the problem, we know immediately that
A + C = B
Then, knowing that A, B, and C are single digit integers, we immediately know that B is 9 and A + C is 9.
Then, knowing that we want ABC to be as large as possible, we quickly find ABC = 990 if A and B can be the same digit, or ABC = 891 if they can't be the same.
|
|
|