.
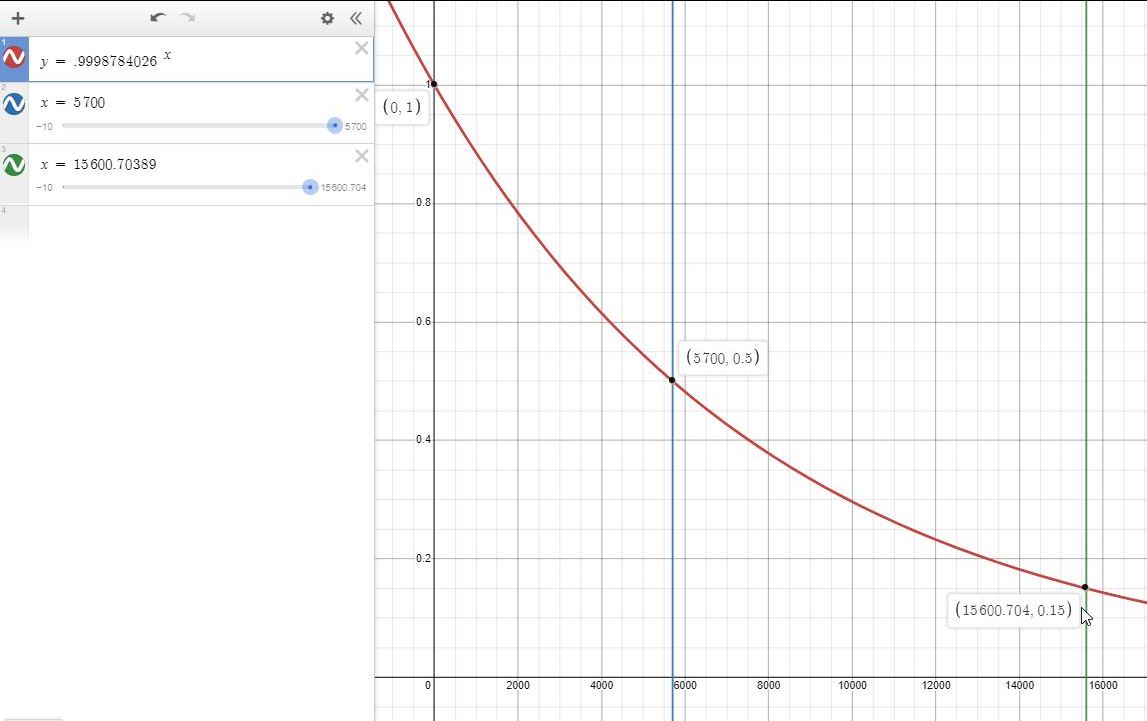
Radioactive Carbon-14, which is found in all living things, has a half-life of 5700 years
and can be used to date fossils. Suppose a fossil contains 15% of the amount of Carbon-14
that the organism contained when it was alive. Calculate the age of the fossil.
~~~~~~~~~~~~~~~~~~~~~~~~
From the condition, you see that half-life period is given of 5700 years.
As soon as you see it, you write the exponential decay function with the base
in the form
m(t) = . (1)
Here m(t) is the current mass of the radioactive Carbon-14; is its initial mass;
t is the time after this organism died.
Notice that the degree at is the ratio of the current time to the given half-time.
+------------------------------------------------+
| So, it is good start and it is RIGHT start. |
+------------------------------------------------+
Next, you are given the ratio ; so, you divide equation (1) by ,
and you get
= .
The ratio is given in the problem: it is 0.15; so, your equation takes the form
0.15 = . (2)
You should solve this exponential equation and find "t" from it.
To solve it, take logarithm base 10 of both sides. Using standard properties of logarithms, you get
log(0.15) = .
It gives you
t = = 15600.7 years.
In carbon dating problem, it is commonly accepted to round the final computed age to closest hundreds of years.
So, your answer is 15600 years.
Solved.
-------------------
What is written in my post, is a standard mantra for this kind of problems.
There is a group of lessons in this site, which covers many similar problems on Carbon dating
- Using logarithms to solve real world problems
- Radioactive decay problems
- Carbon dating problems
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Logarithms".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
///////////////////
Regarding two other posts, I'd like to make couple notices.
To present a solution in a way how @Theo makes in his post, is WRONG way teaching,
because under given conditions, when half-life is given, there is no need to use ekt-form of exponential function, AT ALL.
THEREFORE, to teach as @Theo does in his post, is the same as to teach playing chess game by making obviously wrong first move.
To solve as @josgarithmetic does in his post, is obviously wrong way to teach beginning students.
It is so obvious that does not require any explanations.
Thanks to god, nobody in healthy mind teaches this way.