SOLUTION: The half life of cobalt -60 is 5.27 years. Starting with a sample of 150 mg, after how many years is 20 mg left?

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: The half life of cobalt -60 is 5.27 years. Starting with a sample of 150 mg, after how many years is 20 mg left?      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1191731: The half life of cobalt -60 is 5.27 years. Starting with a sample of 150 mg, after how many years is 20 mg left?
Found 4 solutions by josgarithmetic, Theo, greenestamps, ikleyn:
Answer by josgarithmetic(39613) About Me  (Show Source):
You can put this solution on YOUR website!
Q=150%2A%280.5%29%5E%28t%2F5.27%29

- - - -

log%28%28Q%29%29=log%28%28150%280.5%29%5E%28t%2F5.27%29%29%29

log%28%28Q%29%29=log%28%28150%29%29%2Blog%28%280.5%5E%28t%2F5.27%29%29%29

log%28%28Q%29%29=log%28%28150%29%29%2B%28t%2F5.27%29log%28%280.5%29%29

log%28%28Q%29%29-log%28%28150%29%29=%28t%2F5.27%29log%28%280.5%29%29

5.27%28log%28%28Q%29%29-log%28%28150%29%29%29%2Flog%28%280.5%29%29=t

Description's question is find t when Q=20.

t=5.27%28log%28%2820%29%29-log%28%28150%29%29%29%2Flog%28%280.5%29%29

Answer by Theo(13342) About Me  (Show Source):
You can put this solution on YOUR website!
one of the formula you can use is:
f = p * (1 + r) ^ n
when f = 1 and p = 2 and n = 5.27, you get:
1 = 2 * (1 + r) ^ 5.27
divide both sides of this equation by 2 to get:
.5 = (1 + r) ^ 5.27
take the 5.27th root of both sides of this equation to get:
.5 ^ (1/5.27) = (1 + r)
solve for (1 + r) to get:
(1 + r) = .8767556206.
that's your growth factor per year.

when p = 150 and f = 20, the formula becomes:
20 = 150 * .8767556206 ^ n
divide both sides of this equation by 150 to get:
20/150 = .8767556206 ^ n
take the log of both sides of this equation to get:
log(20/150) = n * log(.8767556206).
divide both sides by log(.8767556206) to get:
log(20/150) / log(.8767556206) = n
solve for n to get:
n = 15.31931344.

.8767556206 and 15.31931344 are rounded to the number of digits that the calculator can display.
i stored these number into memory, which take the answer out to more decimal digits.
this makes it more accurate.
i used the stored number to confirm the answer is correct, even though i am showing you the displayed numbers

2 * .8667556206 ^ 5.27 = 1
1 is 1/2 of 2, so that's your half life.
the growth factor per year is .8667556206.
2 will shrink to 1 in 5.27 years at a yearly growth rate of .8667556206.

150 * .8667556206 ^ 15.31931344 = 20.
150 will shrink to 20 in 15.31931344 years at a yearly growth rate of .8667556206.

note that (1 + r) = .8667556206.
solve for r to get:
r = .8667556206 - 1 = -.1232443794.
that's your annual growth rate.
the life of cobalt -60 is being reduced by approximately 12.32% each year.

the equation can be graphed.
it looks like this.



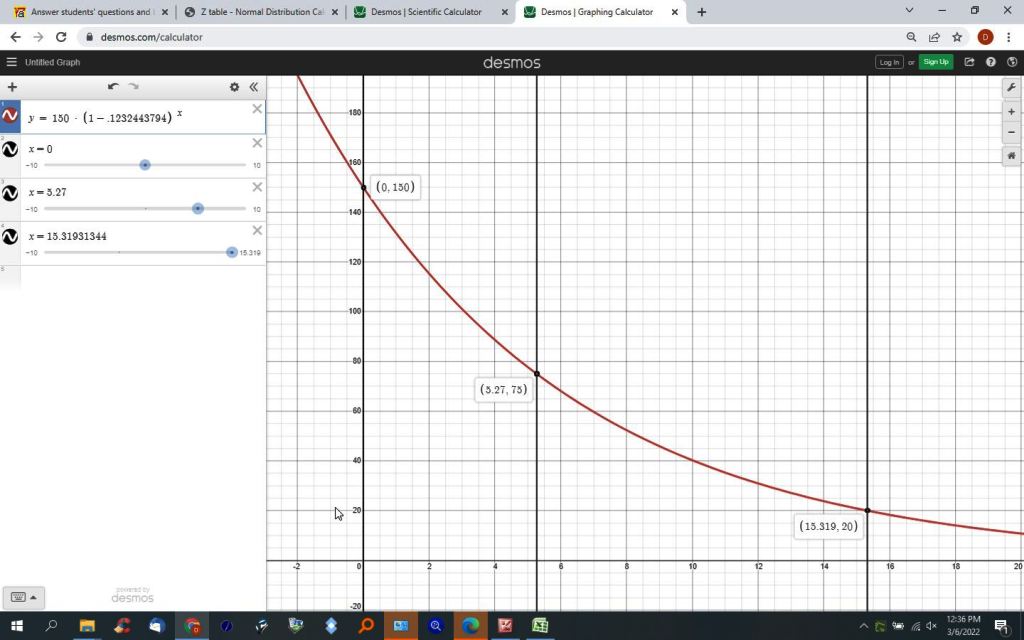
in the graph, you can see that the remaining life of cobalt -60 if 150 years at the beginning, then 75 after 5.27 years, then 20 after 15.3931344 years.










Answer by greenestamps(13195) About Me  (Show Source):
You can put this solution on YOUR website!


Both responses you have received show the same right answer; but the calculations performed in each response are far more convoluted than what is necessary.

You have 150mg of a substance decaying to 20mg in an unknown number of half-lives. The equation is simple:

150%28%281%2F2%29%5En%29=20
150%2F20+=+2%5En

The variable is in an exponent, so use logarithms and use a calculator.

n%2Alog%282%29=log%287.5%29
n+=+log%287.5%29%2Flog%282%29

That number of half-lives, to several decimal places, is 2.90689. Multiply that by the 5.27 years for one half life and you get the answer of approximately 15.32 years.

------------------------------------------------------------------------

It should be noted that radioactive decay is a statistical process; after one half life the amount remaining is APPROXIMATELY half of the original. So keeping 6 or 7 decimal places in the answer to a problem like this is unreasonable.

Answer by ikleyn(52754) About Me  (Show Source):
You can put this solution on YOUR website!
.
The half life of cobalt -60 is 5.27 years. Starting with a sample of 150 mg, after how many years is 20 mg left?
~~~~~~~~~~~~~~~~ 

In terms of the half-life, the general formula for radioactive decay of cobalt-60 is

    M(t) = M%280%29.%281%2F2%29%5E%28t%2F5.27%29

where M(t) is the current mass of the cobalt-60; M(0) is the initial mass,



Since 20 mg of the cobalt-60 remained, you have this equation

    20 = 150%2A%281%2F2%29%5E%28t%2F5.27%29,  which reduces to   20%2F150 = %281%2F2%29%5E%28t%2F5.27%29,

or

    0.133333 = %281%2F2%29%5E%28t%2F5.27%29.
    


To solve it, take logarithm base 10 from both sides. You get an equation 

    log%2810%2C%280.133333%29%29 = %28t%2F5.27%29%2Alog%2810%2C%280.5%29%29 .


Therefore,

     t = 5.27%2A%28log%2810%2C%280.133333%29%29%2Flog%2810%2C%280.5%29%29%29 = 15.32 years  (rounded)


ANSWER.  It will happen in 15.32 years.

Solved.


Regarding precision of the solution,  if the half-life is given with two decimals,
there is no sense to write or calculate the final sough time with the greater precision.

The greater precision is  a  FICTION  in this case.

------------------

On radioactive decay,  see the lesson
    - Radioactive decay problems
in this site.

You will find many similar  (and different)  solved problems there.


        Use this lesson as your handbook,  textbook,  guide,  tutorials, and  (free of charge)  home teacher.
        Learn the subject from there once and for all.


Also,  you have this free of charge online textbook in  ALGEBRA-I  in this site
    - ALGEBRA-I - YOUR ONLINE TEXTBOOK.

The referred lesson is the part of this online textbook under the topic "Logarithms".


Save the link to this online textbook together with its description

Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson

to your archive and use it when it is needed.