SOLUTION: Define your variables and set up the following linear programming problem. You do not have to solve. A farmer has 120 acres of land available for planting crops. It costs $65 t

Question 1175633: Define your variables and set up the following linear programming problem. You do not have to solve.
A farmer has 120 acres of land available for planting crops. It costs $65 to prepare each acre for soybeans and it costs $45 to prepare each acre for wheat. He is not willing to spend more than $2,900 in preparation costs. Each acre of soybeans requires 4 workdays to maintains and each acre of what requires 5 workdays to maintain. The farmer can afford up to a total of 110 workdays. He expects to realize $230 profit per acre of soybean and $155 per acre profit for wheat. How many acres of each crop should he plant in order to maximize his profit? How many acres of soybean and wheat should he plant in order to maximize profit?
Answer by Theo(13342) (Show Source): You can put this solution on YOUR website!
let x = number of acres of soybeans.
let y = number of acres of wheat.

your constraint inequalities are:

x + y <= 120 (acres of land available)
4x + 5y <= 110 (maintenance days)
65x + 45y <= 2900 (prep dollars)
x >= 0, y >= 0 (number of acres can't be negative)

your objective function is 240x + 155y
this is what you want to maximize.

using the desmos.com calculator, you would graph the opposite of the constraint inequalities.

those are:

x + y <= 120
4x + 5y <= 110
65x + 45y <= 2900
x >= 0, y >= 0

the area on the graph that is not shaded is your region of feasibility.
you would evaluate your objective function at each of the corner points of the feasible region to find your maximum profit.

the graph looks like this:

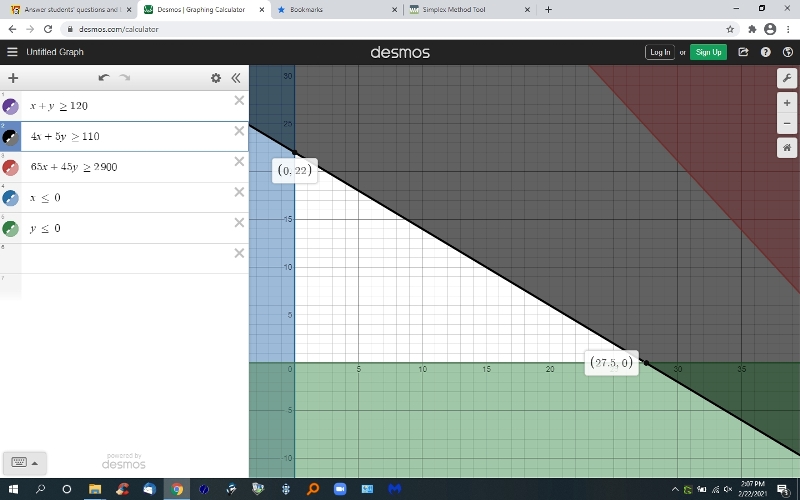
using the simplex method tool, i got the following results.

both tools lead to the answer being 27.5 acres of soybean planted will yield the maximum profit while still keeping within the constraints.

all the constraint inequalities are satisfied at the maximum profit point.

the point on the graph that has the maximum profit is (x,y) = (27.5,0).

65x + 45y = 1787 <= 2900
x + y = 27.5 <= 120
4x + 5y = 27.5 * 4 = 110 <= 110 *****

maximum profit is 27.5 * 230 = 6325.

it appears the maintenance days constraint is the limiting factor.

RELATED QUESTIONS
This is Linear programming pls help me! :( After making various presentations to... (answered by KMST)

Formulate but do not solve the following exercise as a linear programming problem. A (answered by stanbon)

Formulate but do not solve the following exercise as a linear programming problem. A... (answered by solver91311)

According to data from a Texas agricultural report, the amounts of nitrogen (lb/acre),... (answered by chessace)

This is Linear Programming Pls help us! :( please use 2 variables only x and y thank... (answered by Theo,KMST,ikleyn)

This is Linear Programming Pls help us! :( MILESTONE: Linear Program After making... (answered by Theo)

this is linear programming I am having hard time to understand each step :( pls help me I (answered by stanbon)

After making various presentations to potential investors, MC has finally hit the... (answered by ikleyn)

formulate the following problem as a linear programming problem. Do not solve it! Sky... (answered by Alan3354,ikleyn)