f is the future value
p is the present value
r is the interest rate per time period.
n is the number of time periods.
your time period is in years.
n is equal to 100 years.
r is equal to .05 per year.
p is equal to 1000 pounds.
you want to find f.
your formula becomes f = 1000 * (1 + .05) ^ 100.
solve for f to get f = 131,501.2578
that is indeed greater than 100,000 which is equal to 1,000 * 100.
your statement is therefore accurate.
if you wanted to find out when you actually made 100 times your original amount, you would do the following.
f = 100,000
p = 1,000
r = .05
n = what you want to find.
the same formula is used.
it becomes 100,000 = 1,000 * (1 + .05) ^ n
you want to find n.
you would divide both sides of this equation by 100 to get:
100,000 / 1,000 = (1 + .05) ^ n
simplify to get 100 = (1 + .05) ^ n
take the log of both sides of this equation to get:
log(100) = log((1 + .05) ^ n)
since log((1 + .05) ^ n) = n * log(1 + .05), the formula becomes:
log(100) = n * log(1.05)
divide both sides of this equation by log(1.05) to get:
log(100) / log(1.05) = n
solve for n to get n = 94.38726564
the future value of your investment should be exactly 100 times the initial investment in 94.38726564 years.
confirm this is true by replacing n in the original equation with that value to get:
f = 1,000 * (1 + .05) ^ 94.38726564
solve for f to get f = 100,000.
the solution to when you would actually get exactly 100 times your initial investment is confirmed to be good.
you can also graph the equation to visually see what happens to your investment.
for graphing purposes, the equation becomes y = 1000 * 1.05 ^ x.
this is what the graph looks like.
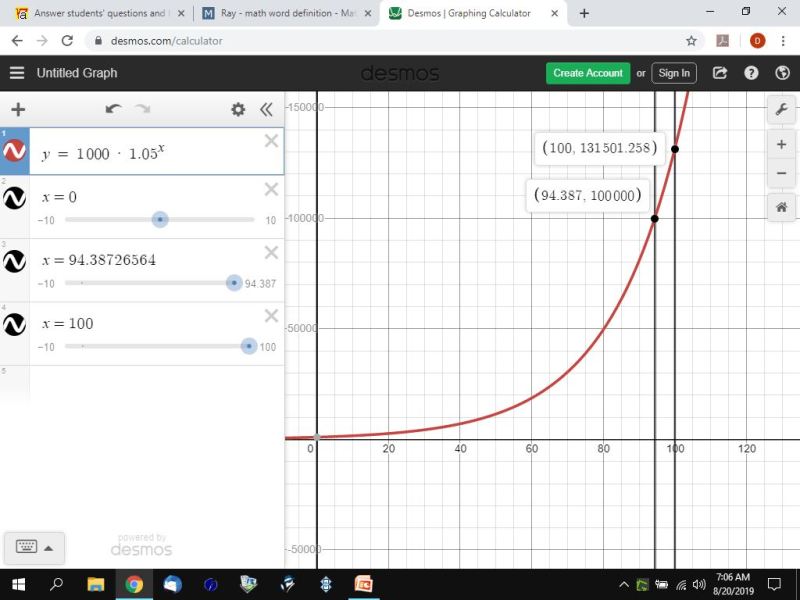
as you can see, your investment really starts taking off after about the 60th year.