SOLUTION: 7. Divide the polynomials below using the long division method. Write your answer in the form of P(x) = Q(x) * D(x) + R(x) i dont know how to type out this equation or the b

Algebra.Com
Question 1122293: 7. Divide the polynomials below using the long division method. Write your answer in the form of P(x) = Q(x) * D(x) + R(x)
i dont know how to type out this equation or the bar thing that it has
https://imgur.com/CjPULcH
Found 3 solutions by josgarithmetic, Theo, rothauserc:
Answer by josgarithmetic(39630)   (Show Source): You can put this solution on YOUR website!
___________________________________________________
x+2 ) 3x^5 +5x^4 -4x^3 +2x^2 +7x +3

"pre" tags:
leftarrow pre rightarrow theExpressioToFormat leftarrow forwardslash pre rightarrow 

    ___________________________________________________
x+2 )  3x^5    +5x^4    -4x^3    +2x^2    +7x     +3




The process works like ordinary long division after that. 
       3x^4
    ___________________________________________________
x+2 )  3x^5    +5x^4    -4x^3    +2x^2    +7x     +3 
       3x^5    6x^4
      --------------
        0     -x^4
and then you keep going as you learned earlier...



       3x^4    -x^3     -2x^2     6x      -5
    ___________________________________________________
x+2 )  3x^5    +5x^4    -4x^3    +2x^2    +7x     +3 
       3x^5    6x^4
      --------------
        0     -x^4
              -x^4      -2x^3
             -----------------
               0       -2x^3      +2x^2
                       -x^3       -4x^2
                      ------------------
                         0        6x^2    +7x
                                  6x^2    12x
                                 ------------
                                   0     -5x     +3
                                         -5x     -10
                                         -----------
                                                13
Remainder is 13.


Answer by Theo(13342)   (Show Source): You can put this solution on YOUR website!
my worksheet is shown below:

$$$

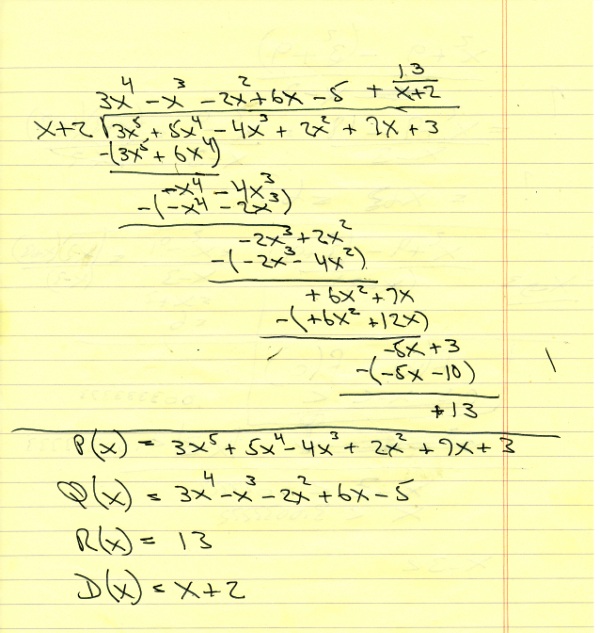
instruction on how to do long division can be found through the following link.

https://www.purplemath.com/modules/polydiv2.htm

to start, i divided 3x^5 by x to get 3x^4.

this was placed in the quotient area above the division line.

i then multiplied (x + 2) by 3x^4 to get 3x^5 + 6x^4

i then subtracted (3x^5 + 6x^4) from (3x^5 + 5x^4) to get -x^4

i then brought down -4x^3 to get (-x^4 - 4x^3)

i then divided -x^4 by x to get -x^3

this was placed in the quotient area above the division line.

i then multiplied (x + 2) by -x^3 to get (-x^4 - 2x^3)

i then subtracted (-x^4 - 2x^3) from (-x^4 - 4x^3) to get -2x^3

i then brought down 2x^2 to get (-2x^3 + 2x^2)

i then divided (-2x^3 by x to get -2x^2

this was placed in the quotient area above the division line.

i then multiplied (x + 2) by -2x^2 to get (-2x^3 -4x^2)

i then subtracted (-2x^3 - 4x^2) from (2x^3 + 2x^2) to get 6x^2

i then brought down 7x to get (6x^2 + 7x)

i then divided 6x^2 by x to get 6x

this was placed in the quotient area above the division line.

i then multiplied (x + 2 ) by 6x to get (6x^2 + 12x)

i then subtracted (6x^2 + 12x) from (6x^2 + 7x) to get -5x

i then broght down the 3 to get (-5x + 3)

i then divided -5x by x to get -5

this was placed in the quotient area above the division line.

i then multiplied (x + 2) by -5 to get (-5x - 10)

i then subtracted (-5x - 10) from (-5x + 3) to get 13.

that ended the division.

13 was my remainder.

13 can be shown as the reminder, or it can be shown as 13 / (x+2) in the quotient area.

if you read the instruction in the link provided, they will tell you pretty much the same thing.

the division is done by the first element in the divior to the first element in the dividend.

the dividend and divisor must be placed in descending order of degree if they are not already in that order.

there is an online polynomial division calculator that you can use to check your work.

that calculator can be found at https://www.symbolab.com/solver/polynomial-long-division-calculator/%5Cfrac%7B%5Cleft(3x%5E%7B5%7D%2B5x%5E%7B4%7D-4x%5E%7B3%7D%2B2x%5E%7B2%7D%2B7x%2B3%5Cright)%7D%7B%5Cleft(x%2B2%5Cright)%7D

my use of that calculator is shown below.

$$$
$$$
$$$
Answer by rothauserc(4718)   (Show Source): You can put this solution on YOUR website!
x+2 | 3x^5 +5x^4 -4x^3 +2x^2 +7x +3
:
multiply the divisor by 3x^4
:
3x^5 +6x^4
:
subtract from the first two terms of the dividend
:
1) -x^4 -4x^3 +2x^2 +7x +3
:
multiply the divisor by -x^3
:
-x^4 -2x^3
:
subtract from 1)
:
2) -2x^3 +2x^2 +7x +3
:
multiply the divisor by -2x^2
:
-2x^3 -4x^2
:
subtract from 2
:
3) 6x^2 +7x +3
:
multiply the divisor by 6x
:
6x^2 +12x
:
subtract from 3)
:
4) -5x +3
:
multiply the divisor by -5
:
-5x -10
:
subtract from 4)
:
13
:
*****************************************************************************
P(x) = Q(x) * D(x) + R(x)
:
(3x^5 +5x^4 +4x^3 +2x^2 +7x +3) = (3x^4 -x^3 -2x^2 +6x -5) * (x+2) +(13/(x+2)
*****************************************************************************
RELATED QUESTIONS

7. Divide the polynomial below using the long division method. Write your answer in the (answered by solver91311,josgarithmetic)
Long Division. Perform the indicated division using long division. Write answer in form... (answered by stanbon)
Using long division, divided p(x)=-4^3+6x^2+4x-7 by(2x-3). Express your answer in the... (answered by josgarithmetic)
Two polynomials P and D are given. Use either synthetic or long division to divide P(x)by (answered by ikleyn)
Two polynomials P and D are given. Use either synthetic or long division to divide P(x)by (answered by ikleyn)
Two polynomials P and D are given. Use either synthetic or long division to divide P(x)... (answered by josgarithmetic)
Two polynomials P and D are given. Use either synthetic or long division to divide P(x)... (answered by vleith)
Two polynomials P and D are given. Use either synthetic or long division to divide P(x) (answered by ikleyn)
Two polynomials P and D are given. Use either synthetic or long division to divide P(x) (answered by josgarithmetic)