Lesson Solved problems on area of a circle

Algebra ->  Customizable Word Problem Solvers  -> Geometry -> Lesson Solved problems on area of a circle      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

This Lesson (Solved problems on area of a circle) was created by by ikleyn(52786) About Me : View Source, Show
About ikleyn:

Solved problems on area of a circle


In this lesson you will find typical solved problems on area of a circle.

Problem 1

Find the area of a circle which has the radius of  5 cm.

Solution

Use the formula above for the area of a circle via its radius.  It gives                            
S = pi.r%5E2 = 3.14159%2A5%5E2 = 3.14159%2A25 = 78.540 cm%5E2.

Answer.  The area of the circle is  78.54 cm%5E2.


Figure 1.  To the  Problem 1


Problem 2

Find the area of a ring concluded between two concentric circles that have the radii of  10 cm  and  8 cm.

Solution

We are given two concentric circles that have the common center  (Figure 2).              
The larger circle has the radius of  R = 10 cm  and  the smaller circle has the
radius of  r = 8 cm.  We need to find the area of the ring concluded between
these two circles.

The larger circle has the area   S = pi%2AR%5E2 = 3.14159%2A100 = 314.159 cm%5E2.
The smaller circle has the area   s = pi%2Ar%5E2 = 3.14159%2A64 = 201.062 cm%5E2.
The area of the ring is the difference of the areas of the circles:
S%5Bring%5D = S - s = 314.159 - 201.062 = 113.097 cm%5E2.


Figure 2.  To the  Problem 2

Answer.  The area of the ring is  113.097 cm%5E2.


Problem 3

Find the area of the circle which is inscribed in the  90°-sector of the circle with the radius of  10 cm.

Solution

We are given a  90°-sector of the circle with the radius of  10 cm  and the              
smaller circle,  which is inscribed in the sector  (Figure 3a).              
The smaller circle touches the radii of the sector,  as well as the larger
circle  (Figure 3a).  We need to find the area of the smaller circle.

Let us draw the angle bisector  OB  of the given sectorial angle of  90°
(Figure 3b),  where the point  B  lies on the larger circle.  It is clear that
the angle bisector  OB  passes through the center  A  of the inscribed
circle.  It is also clear from the symmetry that the point  B  is the
tangent point of the two circles.



Figure 3a. To the Problem 3    




Figure 3b. To the solution
      of the Problem 3

Now,  since the angle  LCOA  is of 45°,  the hypotenuse  OA  is  sqrt%282%29|AC| = sqrt%282%29%2Ar.  Therefore,  R  is:
R = |OA| + r = sqrt%282%29r + r = %281+%2B+sqrt%282%29%29%2Ar.

In other words,  r = R%2F%281+%2B+sqrt%282%29%29.  Hence,  in our case,  r = 10%2F%281+%2B+sqrt%282%29%29 = 4.1421 cm.
It implies that the area of the smaller circle is pi%2Ar%5E2 = pi%2A%28R%2F%281+%2B+sqrt%282%29%29%29%5E2 = pi%2A4.1421%5E2 = 3.14159%2A17.1573 = 53.901 cm%5E2 (approximately).
Answer.  The area of the smaller circle is  53.901 cm%5E2 (approximately).


Problem 4

Find the area of a semicircle inscribed in a triangle with the side measures of                  
13 cm,  14 cm  and  15 cm  in a way that the center and the diameter of the
semicircle lie on the side of the measure  14 cm  of the triangle  (Figure 4a).

Solution

Let the triangle  DELTAABC  be our triangle with the side measures  a = 13 cm,
b = 15 cm  and  c = 14 cm,  and let the point  O  be the center of the inscribed
semicircle  (Figure 4a).

Note that the point  O  lies in the angle bisector of the angle  LC  of the triangle,
since the semicircle is inscribed in the angle  LC.  Thus the point  O  is the
intersection point of this angle bisector and the triangle side  AB  (Figure 4b).

Now,  let us draw the radii  OD  and  OE  from the center of the semicircle to the
tangent points  D  an  E  at the sides  AC  and  BC  of the triangle,  respectively.


    Figure 4a. To the Problem 4          



    Figure 4b. To the solution
          of the Problem 4

These radii are perpendicular to the sides  AC  and  BC  of the triangle according to the property proved in the lesson  A tangent line to a circle is perpendicular to the radius drawn to the tangent point  under the topic  Circles and their properties  of the section  Geometry  in this site.  Therefore,  the radii  OD  and  OE  are the altitudes in the triangles  DELTAACO  and  DELTABCO  respectively.

Next,  you can calculate the area of the triangle  DELTAABC  by the two ways.  From one side,  the area of the triangle  DELTAABC  is

S%5BABC%5D = = sqrt%2821%2A%2821-13%29%2A%2821-14%29%2A%2821-15%29%29 = sqrt%2821%2A8%2A7%2A6%29 = 84 cm%5E2            (1)

by the Heron's formula,  where 21 = %28a%2Bb%2Bc%29%2F2  is the semiperimeter of the triangle.  From the other side,  the area of the triangle  DELTAABC  is the sum of the areas of the triangles  DELTAACO  and  DELTABCO,  i.e.

S%5BABC%5D = a%2Ar%2F2 + b%2Ar%2F2.            (2)

where  r  is the radius of the semicircle.  From the equations  (1)  and  (2) 

r = 2%2F%28a+%2B+b%29* = 2%2F%2813%2B15%29.84 = 84%2F14 = 6 cm.

Hence,  the area of the semicircle is  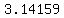1%2F2.pi%2Ar%5E2 = 1%2F2*3.14159*6%5E2 = 56.549 cm%5E2 (approximately).  The solution is completed.

Answer.  The area of the semicircle is  56.549 cm%5E2 (approximately).


My other lessons on the area of a circle,  the area of a sector and the area of a segment of the circle in this site are
    - Area of a circle,
    - Area of a sector  and
    - Area of a segment of the circle
under the topic  Area and surface area  of the section  Geometry,  and
    - Solved problems on area of a sector,
    - Solved problems on area of a segment of the circle  and
    - Solved problems on area of a circle, a sector and a segment of the circle
under the current topic  Geometry  of the section  Word problems.

To navigate over all topics/lessons of the Online Geometry Textbook use this file/link  GEOMETRY - YOUR ONLINE TEXTBOOK.

This lesson has been accessed 4472 times.