This Lesson (Solved problems on volume of spheres) was created by by ikleyn(52787)   : View Source, ShowAbout ikleyn:
Solved problems on volume of spheres
In this lesson you will find typical solved problems on volume of spheres.
The theoretical base for these problems is the lesson Volume of spheres under the topic Volume, metric volume of the section Geometry in this site.
Problem 1Find the volume of a sphere if its radius is of 3 cm.
Solution
The volume of the sphere is
  = =   = =  = =  = 113.097 = 113.097  (approximately). (approximately).
Answer. The volume of the sphere is 113.097  (approximately). (approximately).
Problem 2Find the volume of a composite body comprised of a right circular cylinder and a hemisphere attached center-to-center to one of the cylinder bases (Figure 1) if both the cylinder diameter and the hemisphere diameter are of 10 cm, and the cylinder height is of 20 cm.
Solution
The volume of the composite body under consideration is the sum of the volume
of the cylinder    and the volume of the hemisphere and the volume of the hemisphere   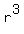 . .
So, the volume of the composite body is equal to
 = =    + +   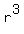 = =  *( *( ) = ) =  = =
= 3.14159*583.33 = 1832.59 (approximately). (approximately).
|

Figure 1. To the Problem 2
|
Answer. The volume of the composite body under consideration is 1832.59  (approximately). (approximately).
Problem 3Find the volume of a composite body comprised of a cone and a hemisphere attached center-to-center to the cone base (Figure 2) if both the cone base diameter and the hemisphere diameter are of 10 cm and the cone height is of 5 cm.
Solution
The volume of the composite body under consideration is the sum of the volume
of the cone     and the volume of the hemisphere and the volume of the hemisphere   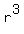 . .
So, the total volume of the composite body is equal to
 = =     + +   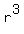 = =   * * = =
=  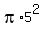 *( *( ) = ) =   * * = =  = 125*3.14159 = = 125*3.14159 =
= 392.7  (approximately). (approximately).
|

Figure 2. To the Problem 3
|
Answer. The volume of the composite body under consideration is 392.7  (approximately). (approximately).
Problem 4Find the volume of a composite body comprised of a cube and a hemisphere attached center-to-center to one of the cube faces (Figure 3) if both the cube edge measure and the hemisphere diameter are of 10 cm.
Solution
The volume of the composite body under consideration is the sum of the volume
of the cube  plus the volume of the hemisphere plus the volume of the hemisphere   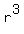 , where , where  = =  = 5 cm. = 5 cm.
So, the volume of the given composite body is equal to
 = =  + +    = =  + +   = 1000 + 261.8 = 1261.8 = 1000 + 261.8 = 1261.8  (approximately). (approximately).
|

Figure 3. To the Problem 4
|
Answer. The volume of the composite body under consideration is 1261.8  (approximately). (approximately).
Problem 5Find the volume of the sphere inscribed in a cone if the base diameter of the cone is of 30 cm and the height of the cone is of 36 cm (Figure 4a).
Solution
Figure 4a shows 3D view of the cone with the inscribed sphere. Figure 4b
shows the axial section of this cone and the inscribed sphere as the isosceles
triangle with the inscribed circle.
The radius of the inscribed sphere in the cone in the Figure 4a is the same
as the radius of the inscribed circle in the triangle in the Figure 4b. So,
instead of determining the radius of the sphere we will find the radius of the
inscribed circle. For it, use the formula  = =  , where , where  is the radius is the radius
of the inscribed circle in a triangle,  is the area of the triangle and is the area of the triangle and  is is
the perimeter of the triangle. The proof of this formula is in the lesson
Proof of the formula for the area of a triangle via the radius of the inscribed
circle under the topic Area and surface area of the section Geometry
in this site.
|

Figure 4a. To the Problem 5
|

Figure 4b. To the solution
of the Problem 5
|
For our isosceles triangle, we have  = =  = 39 cm for its lateral side length, = 39 cm for its lateral side length,  = =  = 108 cm for the perimeter and = 108 cm for the perimeter and  = =   = 540 = 540  for the area. for the area.
Therefore, the radius of the inscribed circle is  = =  = =   in accordance with the formula above. in accordance with the formula above.
Hence, the volume of the sphere inscribed in the cone is   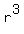 = =   = =  = 1333.33*3.14159 = 4188.79 = 1333.33*3.14159 = 4188.79  . .
Answer. The volume of the sphere inscribed in the cone is 4188.79  (approximately). (approximately).
My lessons on volume of spheres and other 3D solid bodies in this site are
To navigate over all topics/lessons of the Online Geometry Textbook use this file/link GEOMETRY - YOUR ONLINE TEXTBOOK.
This lesson has been accessed 9373 times.
|

