SOLUTION: The angle of elevation of the top of cell tower B from the top of cell tower A is 30 degrees. The angle of depression of the foot of the cell tower B from the top of cell tower A i

Question 884120: The angle of elevation of the top of cell tower B from the top of cell tower A is 30 degrees. The angle of depression of the foot of the cell tower B from the top of cell tower A is 60 degrees. The height of cell tower B is 100 meters. The foot of cell tower A and the foot of cell tower B is in the same horizontal plane.
What is the height of cell tower A?
Answer by Theo(13342) (Show Source): You can put this solution on YOUR website!
the following picture shows the relationship between all the parts.

see below the picture for the analysis.

$$$

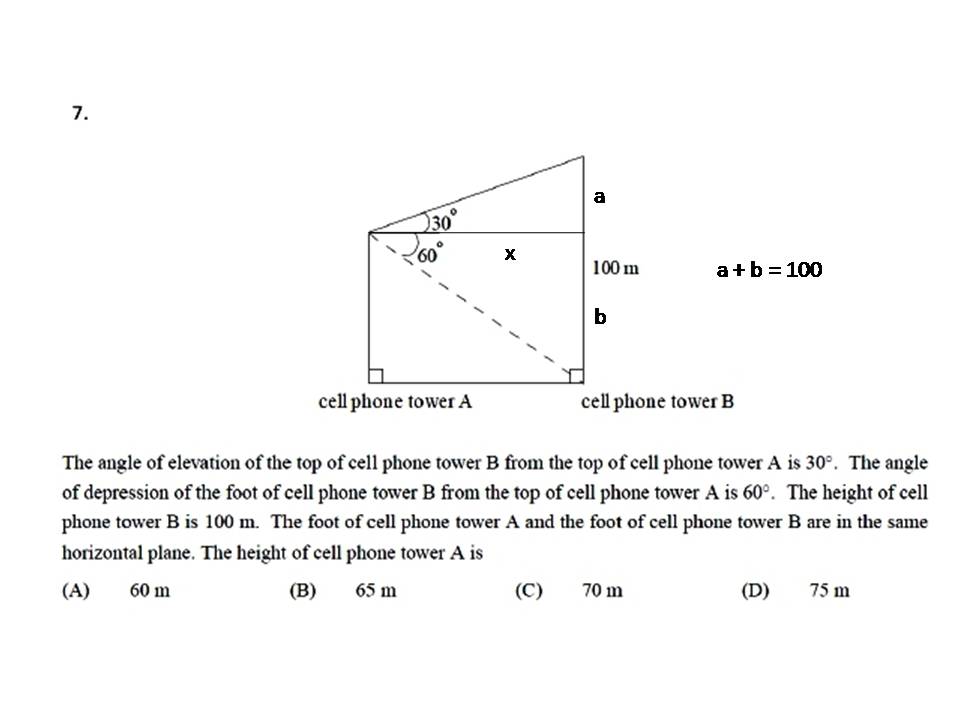
tan(30) = a/x

tan(60) = b/x

solve both these equations for x to get:

x = a/tan(30)

x = b/tan(60)

for ease of presentation, let T30 = tan(30) and T60 = tan(60).

because they both equal x, then they are both equal to each other so you get:

a/T30 = b/T60

multiply both sides of this equation by T30 to get:

a = T30/T60 * b

since a + b = 100, you can solve for b to get b = 100 - a.

substitute for b in the equation of a = T30/T60 * b to get:

a = T30/T60 * (100 - a)

simplify this to get:

a = (T30/T60 * 100) - (T30/T60 * a)

add (T30/T60 * a) to both sides of this equation to get:

a + (T30/T60 * a) = (T30/T60 * 100)

factor out the a on the left side of the equation to get:

a * (1 + T30/T60) = (T30/T60 * 100)

divide both sides of this equation by (1 + T30/T60) to get:

a = (T30/T60 * 100) / (1 + T30/T60)

since T30/T670 = 1/3, you can replace T30/T60 with 1/3 and solve for a to get:

a = (1/3 * 100) / (1 + 1/3) which becomes:

a = (1/3 * 100) / (4/3) which becomes:

a = (1/3) * (3/4) * 100 which becomes:

a = 25

since a + b = 100, this means that b = 75 which means that the height of tower A is equal to 75.

RELATED QUESTIONS
There is a cell phone tower in the field across Tess's house. If she walks 50ft from the... (answered by Theo)

Two office towers are 50 meters apart. From the 14th floor of the shorter tower, the... (answered by stanbon)

The angle of elevation of the top of a tower as observed from A is 30 degrees. At point... (answered by ankor@dixie-net.com)

A surveyor standing W 25 degrees S of a tower measures the angle of elevation of the top... (answered by math_tutor2020)

Jack measures the angle of elevation to the top of a 250 ft high telecommunications tower (answered by josgarithmetic)

from the top of a tower, the angle of depression of a rock is 41 degrees. if the distance (answered by solver91311)

A ranger's tower is located 44 meter from a tall tree. From the top of the tower, the... (answered by josgarithmetic)

Standing 13.3 m away from the base of the tower. Issa measures the angle of elevation to... (answered by Theo)

Angles of Depression/Elevation: From the top of a tower 83 feet high, a man observes that (answered by lynnlo)