SOLUTION: find the center and radius of the circle passes through (2,3), (6,1) and (4,3).

Algebra ->  Customizable Word Problem Solvers  -> Geometry -> SOLUTION: find the center and radius of the circle passes through (2,3), (6,1) and (4,3).      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 771666: find the center and radius of the circle passes through (2,3), (6,1) and (4,3).
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
The center of the circle is at the same distance from the 3 points.
That means it's on the perpendicular bisector of the segments connecting those 3 points.
Points (2,3) and (4,3) are on a horizontal segment with midpoint at (3,3).
The perpendicular bisector of that segment is the vertical line that passes through (3,3), with equation x=3.
All we need now is a second segment and its perpendicular bisector.
The midpoint of the segment connecting (6,1) and (4,3) is
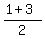(%286%2B4%29%2F2,%281%2B3%29%2F2) or (5,2).
The slope of the line connecting (6,1) and (4,3) is
%283-1%29%2F%284-6%29=2%2F%28-2%29=-1
The slopes of perpendicular line multiply to yield -1, so the slope of the perpendicular bisector to the segment connecting (6,1) and (4,3) is
%28-1%29%2F%28-1%29=1
The perpendicular bisector to the segment connecting (6,1) and (4,3) has the equation
y-2=1%28x-5%29 (in point-slope dorm based on midpoint (5,2).
y-2=1%28x-5%29-->y-2=x-5-->y=x-3
The intersection of the two perpendicular bisectors found is the solution to
system%28x=3%2Cy=x-3%29, and that is system%28x=3%2Cy=0%29, the point (3,0),
The center of the circle is highlight%28%22%283%2C0%29%22%29.
The radius is the distance from that point to any of the 3 given points.
For example, using (4,3),
radius=sqrt%28%284-3%29%5E2%2B%283-0%29%5E2%29-->radius=sqrt%281%5E2%2B3%5E2%29-->radius=sqrt%281%2B9%29-->highlight%28radius=sqrt%2810%29%29.