Question 152354: Hi,
Can someone please review the following, I did the work I just want to make sure it correct before I submit it.
Thank you for your help.
From the given polynomials, identify the polynomials of degree one.
a. 311y - 5 - 43y Since degree is based on the power of the largest variable (or is degree 0 if everything is constants). You have an expression that contains y to a power of 1. So the degree is 1
b. (11y2)1/2 + 14 ( This is a degree 2)
c. 10 + (19)1/2x (This is not a polynomial)
d. 2 + 15x ( This is a degree 1 polynomial)
e. 52y4 + 7x + 2 ( This is not a polynomial)
f. (68)1y1 (This is a degree 1 polynomial)
g. x3 + 3x – 9 ( This is a degree 3 )
h. (2x)1/2 + 4x – 8 (This is a degree 1)
Solve the following:
1. -2x = 3x + 4
-2x = 3x + 4
5x=4 --------> -5*x/5 = 4/(-5)
= -4
5
2. 3x/4 = 6
3x=6*4 , cross multiply:
3x=24 --------> 3*x= 24*8/3 eliminate 3 and 24
x=8
3. y/6 + 1 = 9
y/6 + 1 = 9
y+6/6=9, cross multiply,
y+6=54
y=54-6
y= 48
6 = -2x/4 , cross multiply,
24= -2x -------> 24 * 12/-2 = -2*x/-2 eliminate like terms 24,-2,-2,-2
x= -12
4. 6 = -2x/4
6 = -2x/4
-2x=6*4
-2x=24
x=24/-2
Answer: x=-12
To proof it I did the following:
6=-2*-12/4
6=24/4
6=6
5. Find f(1) for f(x) = 4x3 - 3x2 - x + 2
The problem gives you a "function of x":
f(x) = 4x3 - 3x2 - x + 2
.
Now, to find f(1), it simply asks you to find the value of f(x) when x=1
.
So I , simply substitute in 1 wherever I see the x and solve:
f(x) = 4x^3 - 3x^2 - x + 2
Substituting I get:
f(1) = 4(1)^3 - 3(1)^2 - 1 + 2
f(1) = 4(1) - 3(1) - 1 + 2
f(1) = 4 - 3 - 1 + 2
f(1) = 6 - 4
f(1) = 2 (so f(1)=2)
Answer: f(1)=2
6. A function gives the value of C as 2 × (22/7) × r. Find C when r = 21 cm and r = 84 cm.
plug in 21 for r:
C = 2 × (22/7) × 21
Answer: C = 132 cm
And plug in 84:
C = 2 × (22/7) × 84
Answer: C = 528 cm
Answer by Earlsdon(6294)   (Show Source): (Show Source):
You can put this solution on YOUR website! All of your answers look good except for the first problem, part e.
Given: 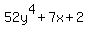 ...You said "This is not a polynomial" Why is it not? ...You said "This is not a polynomial" Why is it not?
It certainly qualifies as a polynomial (a trinomial in this case) because there are no terms with variables in the denominator and no terms with variables under a radical sign.
This polynomial is of degree 4 because of the 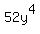
|
|
|