i don't know any other ways.
the graphical solution is shown below:
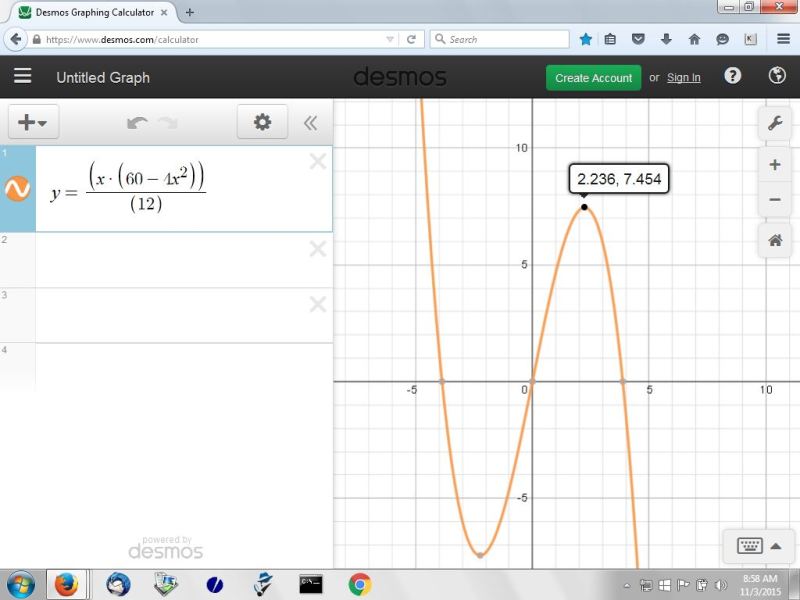
that 2.236 turns out to be sqrt(5).
the value of x is sqrt(5).
the value of y is 7.454
x is the length of a side of the square base.
y is the volume.
the formula for volume is derived as follows:
s = measure of one of the sides of the base.
h = measure of the height.
area of the base = s^2
volume = s^2*h
surface area is derived as follows:
sa = 2*s^2 + 4*h*s
cost of surface area is derived as follows:
cost of the base material is equal to 2 * the area of the base.
cost of the side material is equal to 3 * the area of the sides between the 2 bases.
the total cost is there equal to 2 * area of the bases plus 3 * area of the side faces.
you get total cost = 2 * (2s^2) + 3*(4hs) which becomes:
total cost = 4s^2 + 12hs
since total cost is 60, you get:
60 = 4s^2 + 12hs
in this equation, you can solve for h as follows:
subtract 4s^2 from both sides to get:
60 - 4s^2 = 12hs
divide both sides by 12s to get:
(60-4s^2) / 12s = h
the volume is equal to s^2*h
replace h with (60-4s^2)/12s to get:
volume = s^2 * (60-4s^2)/12s
factor out an s from the numerator and denominator and you get:
volume = s*(60-4s^2)/12
to graph this equation, make volume = y and make s = x.
formula becomes:
y = x*(60-4x^2)/12
this is the equation that was graphed above.
to solve this using calculus, get the derivative of the equation and set it equal to 0 and solve for x to find the maximum point on the graph.
the derivative turns out to be y' = 5-x^2
set it equal to 0 and you get 0 = 5-x^2
add x^2 to both sides to get x^2 = 5
take square root of both sides to get x = +/- sqrt(5).
it has to be sqrt(5) because negative values are not allowed.
the derivative is telling you that you need to evalute your equation at x = sqrt(5) to find the maximum volume.
that turns out to be same as what the graph is showing you.
the more detailed answer is:
x = s = 2.236068
y volume = 7.4535599
round these to x = 2.236 and y = 7.454
x is equal to s which is the width
y is the volume
the volume is s^2*h
you can use this formula to solve for h.
from this formula, solve for h to get h = v/s^2.
that becomes h = 7.4535599/2.236068 = 1.49071195
round to 3 decimal place to get h = 1.491
the dimension of the box with the greatest volume that has a surface area that costs 60 dollars is therefore:
s = 2.236
h = 1.491
if you recall, we made s = x when we graphed it.
when we found x, we automatically found s because they're equivalent to each other.
surface area = 2 * s^2 + 4hs
cost for surface area = 4s^2 + 12hs
when s = 2.236 and h = 1.491, we get cost for surface area = 59.999999999 which rounds to 60.
we got the maximum volume for a box that has a total cost for surface area of 60 dollars.
derivative was found using the following derivative calculator.
the calculator is very useful when you're not sure how to find the derivative.
http://www.derivative-calculator.net/#