y is the value of the car.
x is the number of years from when the car is new.
the y-intercept is the value of the car when x = 0.
this is when the car is new.
the y-intercept is therefore 21000.
m is the average change in the value of the car each year.
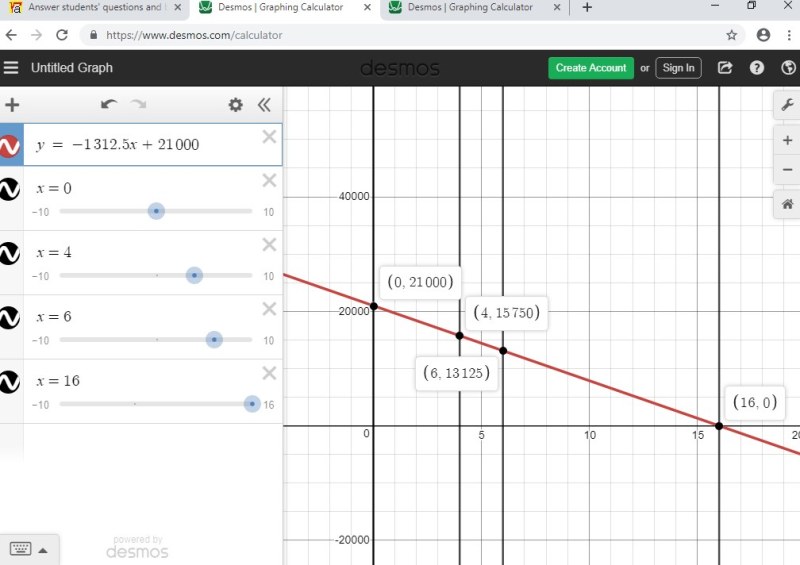
if the value of the car drops from 21000 to 3/4 * 21000 in 4 years, then the slope is (15750 - 21000) / 4 = -1312.5
the equation for straight line depreciation becomes y = -1312.5 + 21000.
the graph of that equation is shown below.
when the value of the car is given by the exponential formula of A * e^(kt), you would create the formula as follows.
the general form of the exponential form, as shown, is V = A * e^(kt)
V is the value of the car after t years have elapsed.
A is the initial value of the car.
e is the scientific constant of 2.718281828.....
t is the number of years.
k will be the interest rate per year.
A is equal to 21000.
when t is 4, V is equal to 15750 (3/4 of the initial value of the car).
the formula becomes 15750 = 21000 * e^(4k).
divide both sides of this formula to get 3/4 = e^(4k)
take the natural log of both sides of this formula to get ln(3/4) = ln(e^4k).
since ln(e^4k) = 4k * ln(e), and since ln(e) is equal to 1, the formula becomes ln(3/4) = 4 * k
divide both sides of this formula by 4 to get ln(3/4) / 4 = k
solve for k to get k = -.0719205181.
the formula becomes V = 21000 * e^(-.0719205181 * t).
to graph this formula,let y = V and let x = t.
the formula becomes y = 21000 * e^(-.0719205181 * x).
the graph of that equation is shown below.
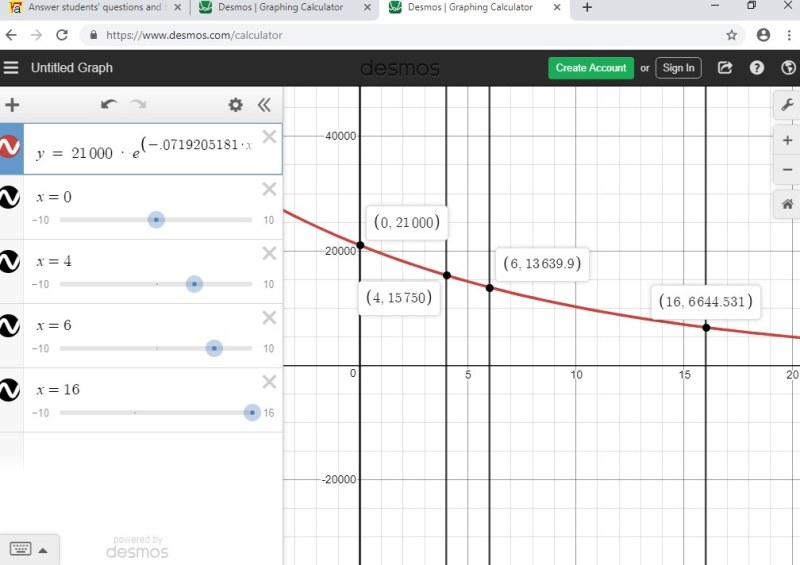
you in see that, in both graphs, when the value of x = 4, the value of the car is 15750.
the graph of the straight line depreciation is a straight line.
the graph of the exponential depreciation is a curve.
the value of the car drops the same amount each year with straight line depreciation.
the value of the car drops by the same percentage each year with exponential depreciation.
the percentage it drops each year is derived from the exponential formula.
the formula is V = A * e^(kt).
k is equal to -.0719205181.
when t = 1, e^(k * t) becomes e^(-.0719205181) which is equal to .9306048591.
each year, the value of the car is .9306048591 * the value of the car in the preceding year.
that's a drop in value of 1 - .9306048591 = .0693951409.
you can confirm this is true by looking at each year.
at year 0,the value is 21000
at year 1,the value is .93... * 21000 = 19542.70...
at year 2, the value is .93... * 19542.70... = 18186.53...
at year 3, the value is .93... * 18186.53... = 16924.47...
at year 4, the value is .93... * 16924.47... = 15750.
it will be exactly 15750 after 4 years because 4 years is how the value of k was determined.
looking at the two graphs, you will see that the value of the car becomes equal to 0 in 16 years with straight line depreciation, while the value of the car is equal to 6644.53... after 16 years with exponential depreciation.
this is because the value of the car drops less and less each year with exponential depreciation.
any questions, write to dtheophilis@gmail.com