SOLUTION: Say a car company sells 20 cars each week at a price of $6400 each. The sales department says that for every increase in $300 in price, sales will fall by one car. The dealer's cos

Question 1011054: Say a car company sells 20 cars each week at a price of $6400 each. The sales department says that for every increase in $300 in price, sales will fall by one car. The dealer's cost of each car is $4000. What price will maximize the profit for the company? What will be the equation be arranged as?
I know that profit is equal to revenue minus expenses but I dont know how to arrange the quadratic equation. Thank you
Answer by Theo(13342) (Show Source): You can put this solution on YOUR website!
let x = the number of cars that will not be sold if the price increases by 300 dollars a car.

let 300x = the number of times the price of a car will be increased by 300 dollars.

the dealer's cost is 4000 per car.

the dealer's profit is the sale price of the car minus the cost.

profit equals revenue minus cost.

the formula for profit will therefore be:

profit = (6400 + 300x) * (20 - x) - 4000 * (20 - x)

let's see what happens:

when x = 0:
profit = 6400 * 20 - 4000 * 20 = 48000

when x = 1:
profit = 6700 * 19 - 4000 * 19 = 51300

when x = 2:
profit = 7000 * 18 - 4000 * 18 = 54000

etc.

the equation of profit = (6400 + 300x) * (20 - x) - 4000 * (20 - x) is a quadratic equation.

simplify it to see what it comes out to be.

after simplification, the equation becomes profit = -300x^2 + 3600x + 48000.

this is a quadratic equation in standard form.

since the standard form of a quadration equation is ax^2 + bx + c = 0, then set this equation to 0 and solve using the quadratic formula amd / or the formula for finding the max / min point of the quadratic equation.

you can also graph the equation to see what it looks like.

setting the equation to 0, you get -300x^2 + 3600x + 48000 = 0

this results in:

a = -300
b = 3600
c = 48000

the quadratic formuls is:

                 x = (-b plus or minus sqrt(b^2 - 4ac)
                     ---------------------------------
                                  (2a)

the formula for the value of x for the max / min point is:

                  x = (-b)
                      ----
                      (2a)

you can solve using these equations, or you can graph the equation and, if you have the right software, it will tell you what the solutions are.

the right software in this case, would be http://www.desmos.com/calculator.

there may be others, but this one is pretty good and fairly easy to use.

the graph of the equation looks like this:

$$$

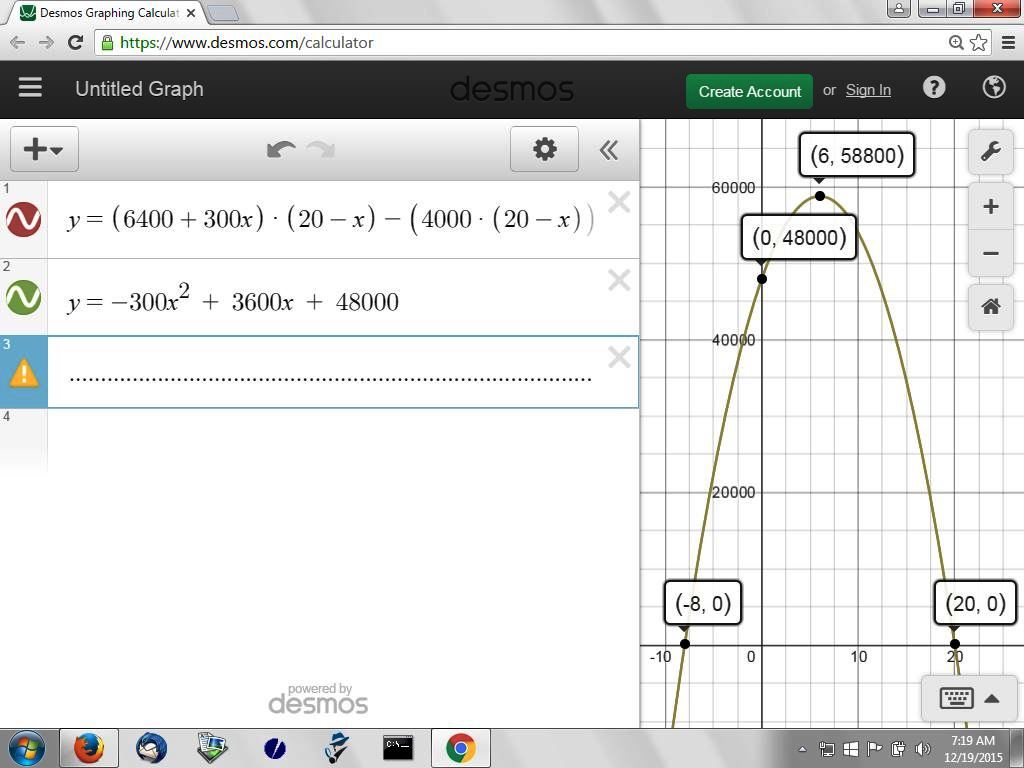
if you solved using the formula, you would get the same answers.

when x = 0, the profit is 48000.
the profit is max at x = 6 when the profit is 58800.
the profit is 0 when x = 20.
on the graph, y represents the profit.

RELATED QUESTIONS
Determine the maximum sales and optimal price. a) Bob can sell 200 cars at $20 000 each (answered by ikleyn)

Determine the maximum sales and optimal price. a) Bob can sell 200 cars at $20 000... (answered by ikleyn)

Determine the maximum sales and optimal price. Tom can sell 200 cars at $20 000 each... (answered by ikleyn)

A community bird-watching society makes and sells simple bird feeders to raise money for... (answered by drcole)

A company can produce a doll at a cost of $5 per dolls. When the company sells the dolls... (answered by josmiceli)

Cali is selling candles at a stand in the mall. She currently sells the candles for $14... (answered by ankor@dixie-net.com)

A club usually sells 1200 shirts a year at $20 each. A survey indicates that for every $2 (answered by ankor@dixie-net.com)

A community bird-watching society makes and sells simple bird feeders to raise money for... (answered by josgarithmetic)

A community bird-watching society makes and sells simple bird feeders to raise money for... (answered by ikleyn)