SOLUTION: Lena has $31.05 in dimes and quarters. The number of dimes is one-fifth the number of quarters. How many of each does she have?

Discussion




With 'coin' problems or 'child/adult ticket' problems or any word problems

that deal with things that can be counted and that each have a fixed value,

you need to proceed in the fashion that I'm about to illustrate.





First, you need an expression or expressions that relate(s) the number of the

things, and then you need an expression or expressions that relate(s) the

value of the things.







Solution





All we know about the number of things is that the number of dimes is one-fifth

the number of quarters.  If we say that the unknown number of quarters is q

and the unknown number of dimes is d, we can express this relationship one of two ways:





Either  or .  I'm going to use the first one; no need

to mess with fractions if you don't have to.  We'll call this the number

equation.





Quarters have a fixed value of 25 cents each, so the value of all the quarters

is 25q cents.  Likewise, the value of the dimes is 10d cents.  Since we have

expressions for the value of the coins in cents, let's convert the total value

of all the coins from $31.05 to 3105 cents. (This time avoiding messy decimals)





, and we'll call this the value equation.





Since we have  without doing any manipulating, we can substitute

 for  in the value equation:







Multiply and add:











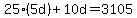
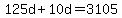
And last, divide:







Telling us that there were 23 dimes.





Substituting this value into  we have:







And now we know there are 115 quarters.







Check Answer





 cents in 115 quarters

 cents in 23 dimes

 total cents = $31.05.  Answer checks.