Question 1139185: The admission fee at an amusement park is $1.25 for children and $6.40 for adults. On a certain day, 333 people entered the park, and the admission fees collected totaled 1163 dollars. How many children and how many adults were admitted?
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52855)   (Show Source):
You can put this solution on YOUR website! .
Let x = # of adult tickets, y = # of children tickets.
From the condition, you have these 2 equations
x + y = 333 (1) (counting tickets)
6.40*x + 1.25*y = 1163 (2) (counting money)
From equation (1), express y = 333 - x and substitute it into equation (2). You will get
6.40x + 1.25*(333-x) = 1163.
Express x and calculate answer
x = 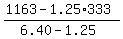 = 145.
Then from equation (1), y = 333 - 145 = 188.
ANSWER. 145 adults tickets and 188 children tickets.
CHECK. 145*6.40 + 188*1.25 = 1163 dollars. ! Correct !
The problem solved using 2-equation setup and the Substitution method.
--------------
It is a standard and typical ticket problem.
For ticket problems, read the lessons
- Using systems of equations to solve problems on tickets
- Three methods for solving standard (typical) problems on tickets
in this site.
From these lessons, learn on how to solve such problems once and for all.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Systems of two linear equations in two unknowns".
Answer by Edwin McCravy(20060)  (Show Source):
You can put this solution on YOUR website!
Put letters for the unknown numbers of children and adults below,
and put the given numbers for the others:
Then solve the system of equations for the two unknowns.
Edwin
|
|
|
