Question 1183899: A group of 35 students performed in a school program. out of the 35,18 sang,19,danced, and 7 sang and danced Venn diagram. thank you
Found 3 solutions by Theo, greenestamps, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! you are stating that.....
there are a total of 35 students.
18 sang
19 danced
7 sand and danced.
your numbers don't add up.
first of all.
if there are 35 students total, and 18 of them sang and 19 of them danced, that gets you a total of 37 students, assuming that none of hem both sang and danced.
in order for there to be 35 students total, 2 of them must have sang and danced.
that would give you 16 who sang only and 17 who danced only and 2 who sang and danced for a total of 35 students.
if you had 18 students who sang and 19 students who danced and 7 who sang and danced, and the 7 who sang and danced were included in the number of those who sang and those who danced, then you would get:
11 sand only and 12 danced only and 7 sang and danced.
that would give you a total of 30 students.
if you had 18 students who sang and 19 students who danced and 7 who sand and danced, and the 7 who sand and danced were not included in the number of those who sang and those who danced, then you would get:
18 sand only and 19 danced only and 7 sang and danced.
that would give you a total of 44 students.
bottom line:
you have a prblem with your numbers.
it could not be 35 students.
it would only be 30 or 44.
here are my two venn diagrams that capture what i think is the case.
the first venn diagram is assuming that the 7 who sang and danced were included in the number of those who sang and those who danced.
the second venn diagram is assuming that the 7 who sang and danced were not included in the number of those who sang and those who danced.
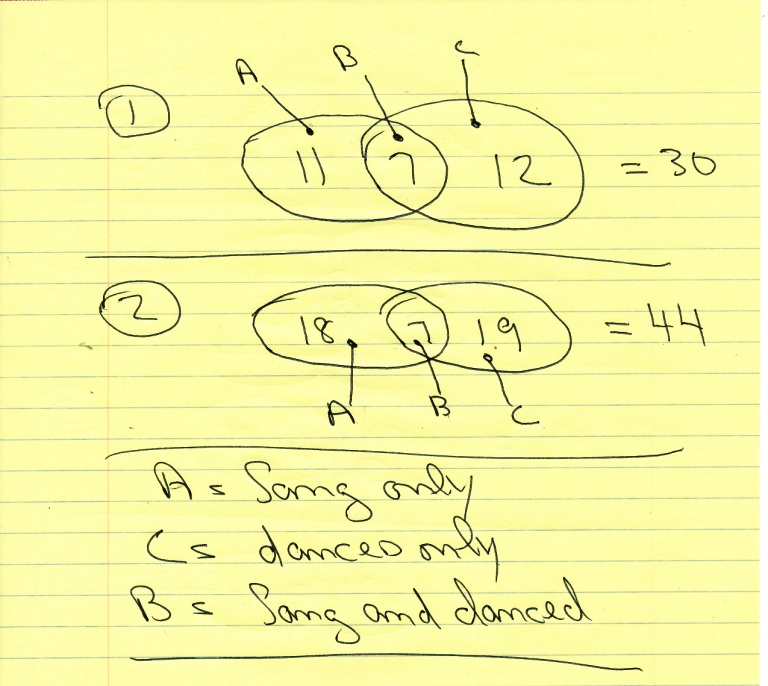
neither of these two options will get you a total of 35 students.
you need to go back and check again what they are asking you to do.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Your post does not contain a question....
18 sang and 7 sang and danced --> 11 sang but did not dance.
19 danced and 7 sang and danced --> 12 danced but did not sing.
So 12 danced only; 11 sang only, and 7 did both.
That makes a total of 30 who did one or the other; so 35-30=5 did neither.
Conclusion:
danced: 12
sang: 11
both: 7
neither: 5
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Having problem like this, first step is to check if the data is consistent.
So, we check how many people are engaged/involved in the described activities.
For it, we calculate the number of those, who are involved in any of singing or dancing.
Their number is 18 + 19 - 7 = 30.
It means that of the group of 35 people, 5 perform some other activities other than singing or dancing.
Now I can answer the problem's questions.
(a) To find how many sang only, subtract from singing those who involved in both singing and dancing
18 - 7 = 11 people sang only. ANSWER
(b) To find how many danced only, subtract from dancing those who involved in both singing and dancing
19 - 7 = 12 people danced only. ANSWER
(c) The number of those who neither sang or danced is 35 - 30 = 5. ANSWER
Solved anf thoroughly explained.
All question are answered.
|
|
|